SPOJ.com - Problem AMBIG

AMBIG - Words on graphs

no tags

Input

The input is a directed (multi)graph.

The first line gives the number of edges M and the number of nodes N (>=2). Then each edge is described by a line of the form "FROM TO LABEL". Nodes (FROM, TO) are numbers in the range 0.. N-1 and labels are also numbers.

All numbers in the input are nonnegative integers <2000.

Output

Print "YES" if there are two distinct walks with the same labelling from node 0 to node 1, otherwise print "NO".

Example 1

Input:
4 4
0 2 0
0 3 0
2 1 1
3 1 2

Output:
NO

Example 2

In this case the shortest labelling that appears on two walks is 0 repeated 10 times.

drawing of example 2

Submit solution!

hide comments

< Previous 1 2 Next >

	:D: 2015-02-28 21:28:25 The problem definitively needs a clarification. I'll try to write a formal description. Lets define an edge as an ordered set {f, t, l, idx}: from, to, label, and index. Two different edges have different indexes, even if all other fields match (let's say it's their line number in the input file). Walk from 'x' to 'y' is an ordered set of edges {e_1, e_2, ..., e_n} where: e_1.f == x e_n.t == y e_i.t == e_(i+1).f for all 'i' in (1, ..., n-1) Problem is asking if there exist two walks from '0' to '1' of equal length ({e_1, ..., e_n} and {f_1, ..., f_n}), such that: e_i.l == f_i.l for all 'i' in (1, ..., n) There exists an 'i' in (1, ..., n) such that e_i.idx != f_i.idx. In other words: there must be at least one different edge between the walks. This can mean some nodes will differ, but there could also be only a "repeated" edge that is treated as distinct. For example for input: 2 2 0 1 0 0 1 0 Answer would be "YES".
	David ©tefan: 2014-12-25 05:30:16 @ebd: "Repeated" edges are distinct edges, yes. Wait, what? This changes everything.
	chipmunk: 2013-08-18 02:12:42 Can there be this type of traversal for NODE! eg. 0 1 1 i.e node 1 has loop so first from 0 -> 1 then again from 1 -> 1.
	Akshay Kumar: 2013-07-12 18:03:52 Is the order of labelling required to be same or can the order be different? for example: are 0 1 2 3 and 2 1 0 3 same?
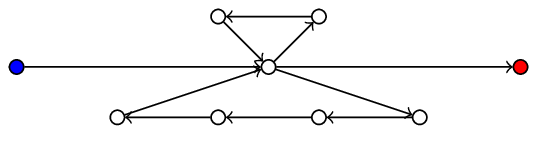
	Erik Lonèarek: 2012-12-30 14:19:18 The picture he meant to provide: Last edit: 2012-12-30 14:26:05
	Goran Zuzic: 2012-05-07 18:15:34 I see a lot of people have some problem understanding the problem, so I'll clarify it the way I've seen it: Mirko once, while travelling from 0 to 1, wrote every label that he saw when he traversed an edge to a notebook in order. He repeated the process another time and found out that the two sequences were identical. Is it possible that the routes he took on the two occasions weren't identical?
	sava: 2012-04-12 17:00:50 Do we have to pass all edges with same label???
	NguyÃªn: 2012-04-04 18:34:56 Is it possible that a walk contains repeated node? For ex: 0-2-3-0-1
	Rita Cristian: 2012-04-01 23:30:25 Last edit: 2012-04-01 23:34:04
	Radu Grigore: 2012-01-03 15:54:55 @ebd: "Repeated" edges are distinct edges, yes. @Aleksa: I don't understand the question.

Submit solution!

Added by:	Radu Grigore
Date:	2009-09-29
Time limit:	1s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	All except: ERL GOSU NODEJS PERL6 VB.NET
Resource:	S Even, On Information Lossless Automata of Finite Order, 1965