FBRIDGES - Factory of Bridges
Original statement in spanish at http://www.dc.uba.ar/events/icpc/download/problems/taip2011-problems.pdf
In the Central Area of Macedonia there is a river following the East-West direction. The region's inhabitants want to build a bridge that crosses the river in the North-South direction, a task for which they have contracted the cheapest bridge factory they know, the Short Bridge Construction Company. As shown by its name, this construction company specializes in building the shortest possible bridges for each river.
The first thing that the company does is to model the river's shores (Northern and Southern). Each of these is considered as being formed by semicircles of varying radii, alternatively oriented to one side or the other, with all their centers collinear. The two lines that are defined by the centers of the semicircles of each shore have the East-West direction, and are separated by a distance A one from the other. The value A is called the width of the river. Note that both shores are aligned, that is, the Northern shore neither begins nor ends further to the West or to the East than the Southern shore.
In the following figure you can see the model of a certain river. In the Northern shore the semicircle furthest to the West is oriented to the North, whereas in the Southern shore the semicircle furthest to the West is oriented to the South. In each shore the orientations of the following semicircles alternate. The shortest possible bridge in the North-South direction is the one shown.
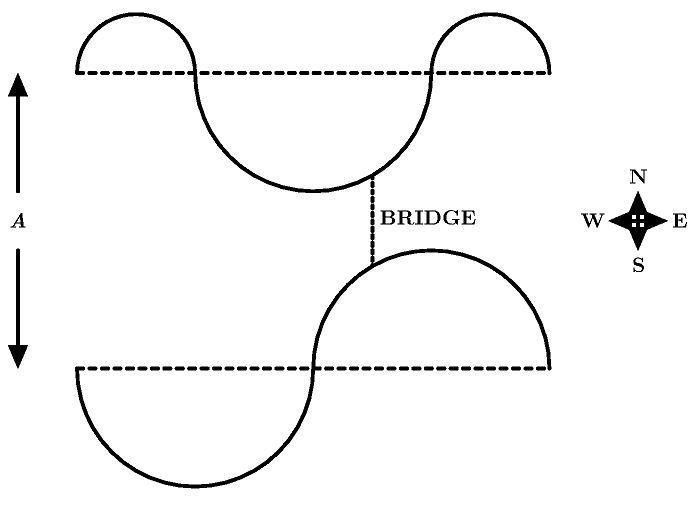
Your task is to help the construction company finding the length of the shortest possible bridge connecting both shores of the river in the North-South direction.
Input
The input contains several test cases. Each test case is described by three lines. The first line contains an integer number A, denoting the width of the river in meters (3 <= A <= 104). The second line describes the Northern shore of the river, while the third line describes its Southern shore.
The description of each shore begins with an integer number C giving the number of semicircles that are used to model that shore (1 <= C <= 1000). This is followed by a character "N" or "S", meaning that the semicircle furthest to the West in this shore is oriented to the North or to the South, respectively. The description ends with C integer numbers R_i, representing the radii in meters of the semicircles that form the shore (1 <= R_i < A/2 for 1 <= i <= C). The semicircles are given in order, from the one furthest to the West (radius R_1) to the one furthest to the East (radius R_C). The orientations of the semicircles alternate between North and South after the first semicircle, whose orientation is given as described above. Assume that in each test case both shores are aligned, which implies that the sum of the radii of the semicircles forming each shore is the same.
The end of the input is denoted by a line containing the number -1.
Output
For each test case, print a single line containing a rational number representing the length in meters of the shortest bridge that connects both shores of the given river in the North-South direction. Round the result to the nearest rational number with 2 decimal digits. In case of ties, round up. Note that you should always print 2 digits after the dot, even if this means ending with a zero.
Example
Input:
5 3 N 1 2 1 2 S 2 2 3 1 N 1 1 S 1 3 1 S 1 1 N 1 -1
Output:
1.54 3.00 1.00
| Added by: | Pablo Ariel Heiber |
| Date: | 2011-10-04 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Argentinian Programming Tournament 2011 |

 RSS
RSS