FISHER - Fishmonger
 A fishmonger wants to bring his goods from the port to the market. On his route he has to traverse an area with many tiny city states. Of course he has to pay a toll at each border.
A fishmonger wants to bring his goods from the port to the market. On his route he has to traverse an area with many tiny city states. Of course he has to pay a toll at each border.
Because he is a good business man, he wants to choose the route in such a way that he has to pay as little money for tolls as possible. On the other hand, he has to be at the market within a certain time, otherwise his fish start to smell.
Input
The first line contains the number of states n and available time t. The first state is the port, the last state is the market. After this line there are n lines with n numbers each, specifying for each state the travel time to the i-th state. This table is terminated with an empty line. The table of the tolls follows in the same format.
n is at least 3 and at most 50. The time available is less than 1000. All numbers are integers.
There are many test cases separated by an empty line. Input terminates with number of states and time equal 0 0.
Output
For each test case your program should print on one line the total amount of tolls followed by the actual travelling time.
Example
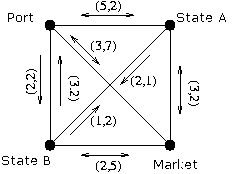
Sample input: 4 7 0 5 2 3 5 0 2 3 3 1 0 2 3 3 2 0 0 2 2 7 2 0 1 2 2 2 0 5 7 2 5 0 0 0 Sample output: 6 6
This corresponds to the following situation, the connections are labeled with (time, toll):
hide comments
|
|
halym2007:
2023-12-02 08:38:22
nice problem |
|
|
pratik_0316:
2021-06-24 11:00:33
dfs pruning !! |
|
|
thanos_tapras:
2020-04-30 17:54:38
Nice dp on graph |
|
|
anandksbiw:
2020-01-30 12:53:42
what is the approach of solving this problem using dijkstra algo? |
|
|
dkkv0000:
2020-01-21 13:16:26
0-1 knapsack |
|
|
sandeepd:
2019-12-11 18:14:00
Nice problem. Last edit: 2019-12-11 18:14:13 |
|
|
aritra741:
2019-07-19 09:18:56
Could anyone suggest more problems like this? |
|
|
aarls:
2019-07-17 18:28:55
can anyone tell how to do this with (DP Knapsack)...? Last edit: 2019-07-18 07:41:54 |
|
|
lamia2658:
2018-08-29 10:33:00
shortest path makes it easy.. ;) |
|
|
amulyagaur:
2017-12-19 06:02:51
submit the same code for FPOLICE also and get 2 ACs within few seconds :) |
| Added by: | Michał Czuczman |
| Date: | 2004-07-07 |
| Time limit: | 3s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | Swiss Olympiad in Informatics 2004 |

 RSS
RSS