HIST2 - Histogram
In statistics, a histogram is a graphical display of tabulated frequencies, shown as bars. It shows what proportion of cases fall into each of several categories. It is a polygon composed of a sequence of rectangles aligned at a common base line. In this problem all rectangles have a width of unit length. But their heights are distinct. Some permutation of the heights will give the maximum perimeter. Your task is to find the maximum perimeter of the histogram and the number of permutations that give the maximum perimeter.
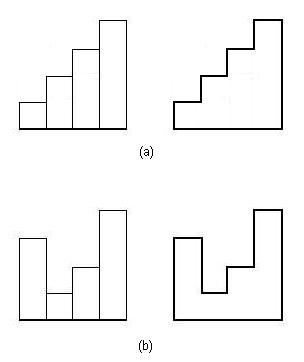
In the image Figure (a) shows a histogram with heights {1, 2, 3, 4} (1st sample testcase) and has a perimeter of 16 units. Figure (b) shows one of the permutations {3, 1, 2, 4} having the maximum perimeter of 20 units.
Input
Input consists of multiple test cases. Each test case describes a histogram and starts with an integer N, 2 ≤ N ≤ 15, denoting the number of rectangles it is composed of. Next line consists of N space separated positive integers representing the heights of the rectangles. All heights are distinct and less than or equal to 100. N=0 indicates the end of tests. There are at most 50 test cases.
For each test case output the maximum possible perimeter of the histogram and the number of permutations that give maximum perimeter in a single line, separated by a single space.
Example
Input: 4 1 2 3 4 3 2 6 5 0 Output: 20 8 24 2
hide comments
|
|
itssstrange:
2022-09-22 20:21:01
Yeah bro I am also getting it wrong
|
|
|
ppap_1264589:
2021-05-14 07:02:00
Dp Bitmask. |
|
|
debarghya4469:
2021-04-24 14:19:38
dp[20][(1<<20)] gives TLE while dp[19][1<<20] passes. Had hard time debugging. |
|
|
vkgainz:
2020-11-08 19:55:46
dubs
|
|
|
scolar_fuad:
2020-01-05 16:03:47
nice bitmask+dp
|
|
|
mac1309:
2019-07-17 20:57:15
solving by bit-masking requires patience and implementation skill. |
|
|
sultania23:
2018-12-23 15:33:03
Good One for learning BitMasking..
|
|
|
amulyagaur:
2018-06-15 10:44:24
1000th solver! |
|
|
amrit_saini:
2017-09-26 20:42:13
Can be done wthout dp or bitmasking using logic of factorial. |
|
|
sucide:
2017-06-13 20:35:46
Ac in one go ,,,
|
| Added by: | Swarnaprakash |
| Date: | 2008-11-29 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 |
| Resource: | Kurukshetra 09 OPC |

 RSS
RSS