HOUSEBUY - House Buying Optimizations
Bill and Scott are business rivals. Each of them wishes to buy a house in Javaville, but they want to live as far away from each other as possible. Since Javaville is a relatively new town, there are no maps available yet; instead, information about homes and other buildings has been collected by word of mouth and provided to both Bill and Scott. This information consists of building addresses and distances between buildings. All of the information is consistent, although it may be incomplete or redundant.
The streets in Javaville are laid out in a rectangular grid of m east/west streets (named ‘A’, ‘B’, ‘C’...) and n north/south streets (numbered ‘0’, ‘1’, ‘2’...), where m and n are each between 2 and 10. Every building (either a house or some other building, such as a post office or school) in Javaville is at the intersection of two streets, and no two buildings are located at the same intersection. Some intersections have no buildings at all. All distances are measured in terms of the smallest number of whole blocks that must be traversed north, south, east, and/or west to get from one intersection to another intersection.
Here is some sample information that might be provided to Bill and Scott by various reliable sources:
- There are 5 east/west streets and 5 north/south streets.
- House1 is located at intersection A0.
- The post office is located at intersection A4.
- The school is at a distance of 4 blocks from house1.
- House2 is at a distance of 6 blocks from the post office.
- The school is at a distance of 6 blocks from the post office.
- House3 is at a distance of 6 blocks from the post office.
From this we can see that there are two possible maps of Javaville — see Figure 1.
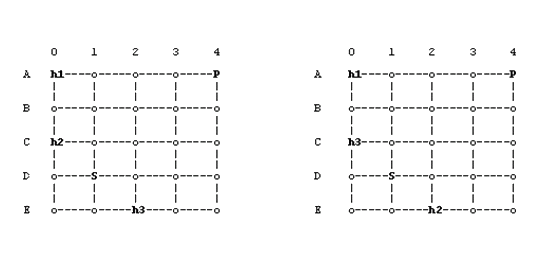
Figure 1: h1, h2, h3 = houses, P = post office, S = school
We see that the locations of house1, the post office, and the school are fixed, but house2 could beat either C0 or E2, and house3 could be at either C0 or E2. Clearly there is always a pair of houses separated by 6 blocks (house1 is always 6 blocks from the furthest house), but the best distance we can guarantee for any specific pair of houses is 4 (since house2 is always 4 blocks away from house3). We would report this information to Bill and Scott, telling them that, even though a separation of 6 is always achievable, the safest recommendation that we are able to make for specific houses is to have one of them purchase house2 and have the other purchase house3. (We assume that Bill and Scott will consult with one another before purchasing their houses in order to guarantee that one of our recommendations is followed.)
Bill and Scott would like you to write a program that will take location and distance information about buildings and determine two quantities, D and D. D is the minimum, over all possible valid arrangements of buildings, of the largest house separation in each arrangement. D is the maximum value for which there exists at least one pair of houses i and j that are guaranteed to be separated by a distance of at least D′. In the latter case, you should list all pairs of houses that are guaranteed to be separated by at least D blocks.
More precisely:
Define the diameter d(S) of a feasible urban layout S as the distance between the two most distant residential homes in the layout. For the two residential houses i, j, define their safety factor: e[i, j] is defined as the minimum value of the distance between residential houses i and j in all feasible urban layouts. Bill and Scott want you to write a program that calculates D and D' based on the information they collect, where
- D = min {d (S)} over all layouts S;
- D' = max {e[i, j]} over all pairs (i, j).
At the same time you also have to give the safest purchase recommendations: that is, all pairs (i, j) meeting e[i, j] = D' for residential houses i and j.
For the above example, the first layout has d(S1) = 6, while the second layout has d(S2) = 6. The safety factor between each two residential houses is respectively: e[1, 2] = 2, e[1, 3] = 2, e[2, 3] = 4. Then:
- D = min {d (S1), d (S2)} = 6, and
- D' = max {e[1, 2], e[1, 3], e[2, 3]} = Purchase recommendations are: house 2 and house 3.
Input
The input will consist of one or more descriptions. Each description will begin with a line containing two positive integers, m and n, representing the number of blocks in each direction (2 ≤ m, n ≤10). Each description will end with a line containing the single word ‘END’ in uppercase. The entire data set will end with a line containing a pair of zeros.
The remaining lines in each data set will be in one of the following two formats:
name LOCATION r c
or
name DISTANCE d name2
where name and name2 are strings containing only digits and lowercase alphabetic characters, each of length at most 10; r is an uppercase letter between ‘A ’ and ‘J ’; c is a digit; and d is a positive integer. If the first five characters of a name are the lowercase letters ‘house ’ then it is a candidate for selection as a home for Bill or Scott; otherwise it stands for some non-residential building. In a ‘DISTANCE’ specification, name2 will always be the name of some building that has occurred previously in this data set as the first name on one of the data lines (in other words, there are no forward references to buildings in ‘DISTANCE’ constraints). Each description is consistent (i.e., there is at least one way to lay out the houses and other buildings in a way consistent with the description). Each description will include information about at least two distinct houses. At most 25 distinct building names will occur in each description, and there will be at most 50 constraints (‘LOCATION’ or ‘DISTANCE’) for each description.
Output
For each description, the output will consist of D, followed by value of D', and then a list of all pairs of houses with maximum guaranteed separation D′ (which might be smaller than the maximum achievable separation). No pair of houses should be listed more than once. The output should be labeled exactly as shown in the sample output below, with a blank line separating the outputs for consecutive data sets. In each pair, houses should be ordered according to the first time they appear in the input; the list of pairs should be ordered in the same way, sorted by the first element of the pair, then by the second element.
Example
Input: 5 5 house1 LOCATION A 0 postoffice LOCATION A 4 school DISTANCE 4 house1 house2 DISTANCE 6 postoffice school DISTANCE 6 postoffice house3 DISTANCE 6 postoffice END 10 10 house1 LOCATION A 0 building2 DISTANCE 12 house1 building2 DISTANCE 12 house1 house3 DISTANCE 7 house1 building4 DISTANCE 2 house3 building4 DISTANCE 7 building2 building4 DISTANCE 2 house3 house5 DISTANCE 6 building4 building6 DISTANCE 10 building2 building6 DISTANCE 5 building4 building6 DISTANCE 2 house1 house7 DISTANCE 1 house1 house7 DISTANCE 1 house1 building8 DISTANCE 10 house7 house9 DISTANCE 10 building2 house9 DISTANCE 3 building4 building10 DISTANCE 5 house3 building10 DISTANCE 5 house3 house11 DISTANCE 3 building2 building12 DISTANCE 7 house7 building12 DISTANCE 8 house1 building12 DISTANCE 9 building4 building12 DISTANCE 3 house5 house13 DISTANCE 7 building8 house13 DISTANCE 3 house5 building14 DISTANCE 2 building10 building14 DISTANCE 9 building8 house15 DISTANCE 12 building8 house15 DISTANCE 11 building12 house15 DISTANCE 9 building2 house15 DISTANCE 7 house13 building16 DISTANCE 6 building10 building16 DISTANCE 3 house11 building16 DISTANCE 12 house9 building16 DISTANCE 5 house7 house17 DISTANCE 4 house11 house17 DISTANCE 3 building12 building18 DISTANCE 8 building14 building18 DISTANCE 10 building6 building18 DISTANCE 8 building14 building18 DISTANCE 10 building6 house19 DISTANCE 2 house13 house19 DISTANCE 6 building18 house19 DISTANCE 1 house5 building20 DISTANCE 8 building14 END 0 0 Output: 6 4 house2 house3 9 9 house1 house11 house5 house9 house9 house11 house9 house17
hide comments
|
|
[Rampage] Blue.Mary:
2022-08-24 11:16:24
Spoiler: Searching for each valid configuration of all houses mentioned is enough to solve this problem. Last edit: 2022-08-24 11:21:08 |
|
|
stevenwjy:
2017-06-03 09:42:03
Finally got AC on this problem.
|
|
|
Chen Xiaohong:
2017-05-31 17:47:16
BTW, stevenwjy, your code is still giving WA on the following simple case:
|
|
|
Chen Xiaohong:
2017-05-28 07:20:29
Fixed, in the problem description. Thanks for pointing this out.
|
|
|
stevenwjy:
2017-05-26 19:11:34
The input format says :
|
| Added by: | Chen Xiaohong |
| Date: | 2017-05-21 |
| Time limit: | 8s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | CTSC 2002 |

 RSS
RSS