KPMAZE - Maze
The King of Byteland likes Greek mythology very much. The most impressive myth for him is the one about Minotaur. A creature which was imprisoned in a maze-like construction. Now The King wants to have similar maze. He ordered to his architect to build such construction.
The architect decided that maze will have rectangular form. Its floor will be made from large square plates. Also there will be many walls, each of which will separate two common floor plates. From the bird's eye whole construction will look like a grid with some cells separated by walls. The maze should be very tricky, that's why he calls the maze correct if and only if for every two plates there is exactly one path between them. Here path is a sequence of moves between plates that share a common side and are not separated by wall. Each plate can only appear once in a path.
Sooner or later, the architect started his work. After a couple of months he created a rectangular area with H rows and W columns. Also he has built K walls. Sounds perfect but he was seized with a lingering doubt about correctness of his maze.
That's why he asks you to help him. He wants to know how many different correct mazes can be built based on his current maze i.e. you can only add new walls but not to break any of the old ones.
For example (see figure 1.) the maze size is 2x2 and there are no walls. All four ways to complete this maze are shown on the right of the figure (new walls are dashed).

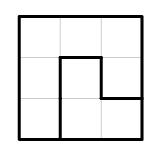
Figure 2. illustrates maze of size 3x3 with 3 walls. There are exactly 4 ways to complete it.

Figure 3. shows the maze that cannot be completed, because there is no path from lower right plate to upper left one.
Input
The first line contains two integer numbers W and H (1 ≤ W, H ≤ 5). Second line contains one integer number K (K ≥ 0). Next K lines contain description of walls. Each wall is determined by two plates it separates. Thus, each line contains four integer numbers: R_1, C_1, R_2 and C_2, here R_1 and C_1 - row and column coordinates of the first plate. Similar, R_2 и C_2 - are coordinates of the second plate (1 ≤ R_1, R_2 ≤ H, 1 ≤ C_1, C_2 ≤ W). Rows are numbered from up to bottom, colums - left to right started from 1. It is guaranteed that all walls are correct and there are no duplicates. Walls that form perimeter of the maze will not be specified.
Output
Output the number of different correct mazes that can be built based on the given one. There should be no leading zeroes.
Example
Input: 2 2 0 Output: 4 Input: 3 3 3 3 1 3 2 2 2 2 3 2 3 3 3 Output: 4 Input: 3 3 5 3 1 3 2 2 2 2 3 2 3 3 3 2 2 2 1 1 2 2 2 Output: 0
hide comments
|
|
ayush:
2014-03-26 18:38:24
please tell what will be the output for following inputs
|
| Added by: | Pavel Kuznetsov |
| Date: | 2007-02-24 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | IT Festival Arkhangelsk 2006 |

 RSS
RSS