Ik geef je een standaard spel van 52 kaarten. Je controleert de kaarten en schudt ze een paar keer door elkaar. Daarna kies je willekeurig vijf kaarten en geeft ze aan mijn assistente. Ze kijkt naar de kaarten en geeft er vier door aan mij. Zonder verpinken kan ik de vijfde kaart benoemen.

Op het eerste gezicht lijkt dit onmogelijk. Er blijven nog 48 kaarten over die de assistente voor mij kan verborgen houden. Door me vier kaarten in een bepaalde volgorde te geven kan ze me slechts één uit $4! = 24$ mogelijke boodschappen doorgeven. Hoe ben ik dan in hemelsnaam in staat om de vijfde kaart te benoemen?

Een deel van het geheim schuilt in het feit dat de assistente kan kiezen welke kaart ze achterhoudt. De groep van vijf kaarten die je hebt uitgekozen moet immers minstens één paar kaarten met dezelfde kleur bevatten (toepassing van het duiventilprincipe). Mijn assistente kiest één van die twee kaarten als de kaart die ze achterhoudt, en geeft me de andere als eerste door. Op die manier weet ik de kleur van de verborgen kaart, en blijven er slechts 12 mogelijkheden over voor de rang van de kaart. Maar mijn assistente kan me nog maar drie kaarten doorgeven, met $3! = 6$ mogelijke boodschappen, waardoor de opdracht onmogelijk lijkt.

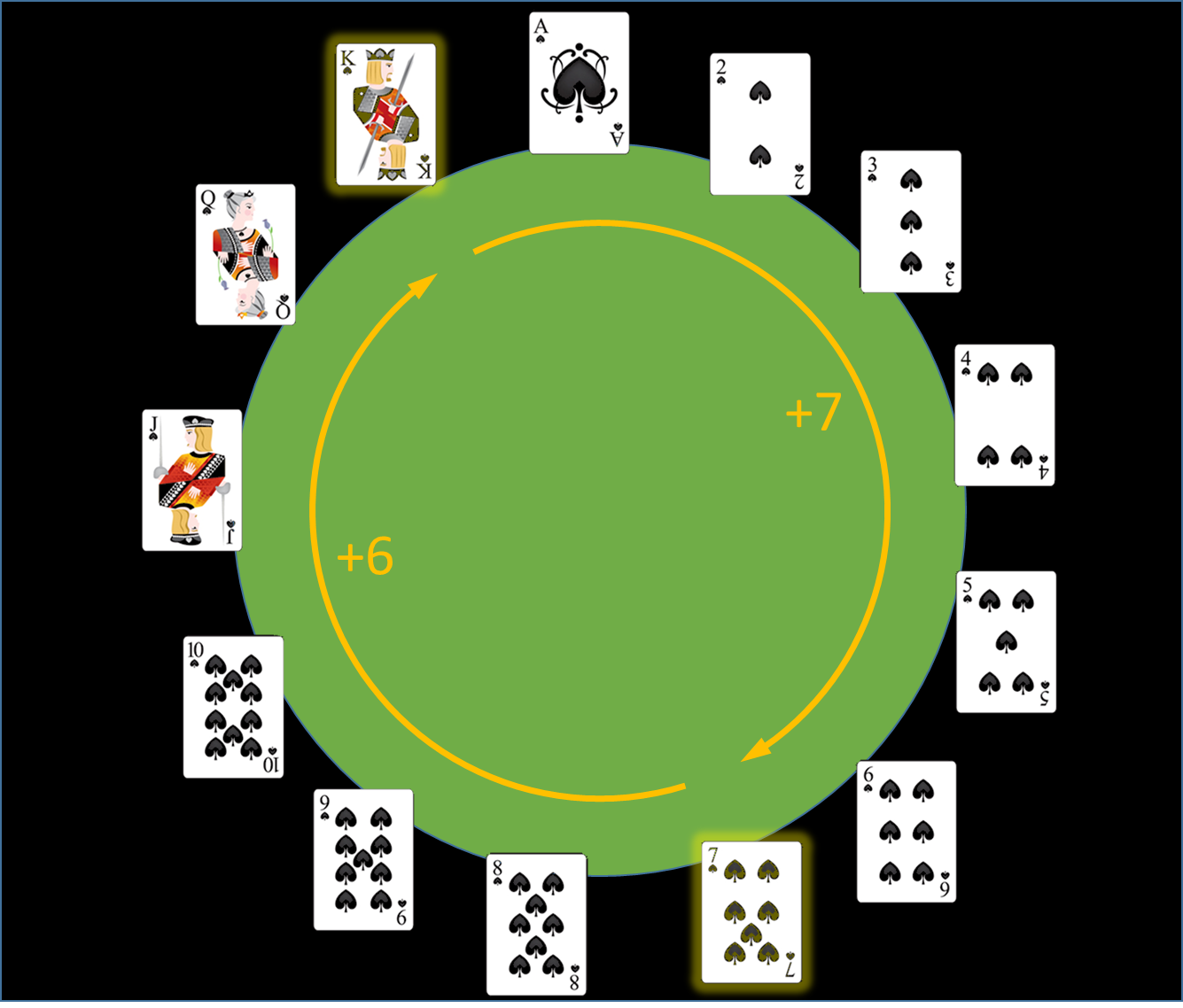
De rest van het geheim zit in de keuze die de assistente kan maken tussen de twee kaarten met dezelfde kleur waarvan ze er één achterhoudt. Beeld je in dat de rangen van de kaarten in wijzerzin neergeschreven worden rond een cirkel (met aas = 1, boer = 11, vrouw = 12 en heer = 13). Voor twee gegeven kaarten is het altijd mogelijk om vanaf de rang van één van de kaarten de rang van de andere kaart te bereiken in ten hoogste 6 stappen door "de kortste route" in wijzerzin langs de cirkel te nemen.

Veronderstel dat de assistente tussen haar vijf kaarten twee kaarten vindt met de kleur schoppen: schoppen heer en schoppen zeven. Als we de opeenvolgende rangen van de kaarten in wijzerzin langs een denkbeeldige cirkel plaatsen, dan vraagt het 7 stappen om vanaf rang heer naar rang zeven te stappen. Het vraagt echter slechts 6 stappen om vanaf rang zeven naar rang heer te stappen. Omdat dit de kortste van de twee afstanden is tussen de schoppen kaarten, zou de assistente in dit geval dus schoppen zeven als eerste kaart doorgeven.

Ik en mijn assistente maken op voorhand de volgende afspraak: we beschouwen een vaste volgorde van de kaarten door ze eerst te sorteren op rang (aas, 2, …, 10, boer, vrouw, heer) en daarna op kleur in de volgorde zoals die gebruikt wordt in bridge: klaveren, ruiten, harten, schoppen. Hierdoor hebben alle kaarten een vaste volgorde, en kan mijn assistente de resterende drie kaarten in één van de zes volgende manieren doorgeven:

$$\begin{eqnarray} \{\textrm{laagste}, \textrm{middelste}, \textrm{hoogste}\} &=& 1 \\
\{\textrm{laagste}, \textrm{hoogste}, \textrm{middelste}\} &=& 2 \\
\{\textrm{middelste}, \textrm{laagste}, \textrm{hoogste}\} &=& 3 \\
\{\textrm{middelste}, \textrm{hoogste}, \textrm{laagste}\} &=& 4 \\
\{\textrm{hoogste}, \textrm{laagste}, \textrm{middelste}\} &=& 5 \\
\{\textrm{hoogste}, \textrm{middelste}, \textrm{laagste}\} &=& 6 \\
\end{eqnarray}$$

Als mijn assistente weet dat ik altijd in wijzerzin de denkbeeldige cirkel met de rangen afloop, dan kan ze de eerste kaart zó kiezen dat die én de kleur van de verborgen kaart aangeeft en ook een specifiek punt op de cirkel aanwijst. De volgorde van de overige drie kaarten vertelt me dan hoeveel stappen ik vanaf dat punt in wijzerzin moet zetten om de rang van de verborgen kaart te achterhalen.

"Als je deze truc nog nooit gezien hebt, dan zal je zeker met verstomming geslagen worden. Lezen hoe het werkt, doet de truc onrecht aan.", schrijft wiskundige Michael Kleber. "Ik ben eeuwige dank verschuldigd aan de bachelorstudent die er en plain public 'Onmogelijk!' uitflapte, net voordat ik de verborgen kaart benoemde." De truc werd voor het eerst in de literatuur uitgelegd in het boek Math Miracles van Wallace Lee uit 1950. Lee schrijft de truc toe aan William Fitch Cheney, een goochelaar uit San Fransisco en houder van het eerste doctoraat in de wiskunde dat werd uitgereikt door het MIT.

Opgave

In deze opgave duiden we de rangen van de kaarten aan met de strings

aas, 2, 3, 4, 5, 6, 7, 8, 9, 10, boer, vrouw, heer

en duiden we de kleuren van de kaarten aan met de strings

klaveren, ruiten, harten, schoppen

Deze reeksen leggen meteen ook de volgorde van de kaarten uit een standaard kaartspel vast, zoals aangegeven in de inleiding. Definieer een klasse Kaart waarmee de kaarten uit het standaard kaartspel kunnen voorgesteld worden. Bij initialisatie van een object van de klasse Kaart moet de rang en de kleur van de kaart opgegeven worden. Indien een ongeldige rang of een ongeldige kleur wordt opgegeven, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige kaart. Zorg ervoor dat de objecten van de klasse Kaart als string voorgesteld worden zoals aangegeven in onderstaand voorbeeld, en dat de zes vergelijkingsoperatoren (<, >, <=, >=, == en !=) kunnen gebruikt worden om twee kaarten met elkaar te vergelijken op basis van hun volgorde in het kaartspel.

Schrijf ook een functie vijfdeKaart waaraan een reeks (een lijst of een tuple) van vier verschillende kaarten (objecten van de klasse Kaart) moet doorgegeven worden. Deze stellen de vier kaarten voor die de assistente doorgeeft aan de goochelaar. De functie moet de kaart teruggeven die de assistente voor de goochelaar verborgen houdt.

Voorbeeld

>>> Kaart('aas', 'schoppen')
Kaart(rang='aas', kleur='schoppen')
>>> print(Kaart('aas', 'schoppen'))
schoppen aas
>>> Kaart('koeken', 'troef')
Traceback (most recent call last):
AssertionError: ongeldige kaart
>>> Kaart('aas', 'schoppen') < Kaart('boer', 'harten')
True
>>> Kaart('aas', 'schoppen') >= Kaart('boer', 'harten')
False

>>> vijfdeKaart([Kaart('7', 'schoppen'), Kaart('vrouw', 'harten'), Kaart('8', 'klaveren'), Kaart('3', 'ruiten')])
Kaart(rang='heer', kleur='schoppen')

Bronnen

• Kleber M (2002). The Best Card Trick. Mathematical Intelligencer 24(1), 9-11.