PROG0280 - Maya numbers
At the beginning of our era, the Maya settled in Central America. In many ways, they were by far the most developed and fascinating civilization of their age. They didn't know wheels or draught animals, but they controlled the art of weaving, architecture and pottery-making like no other. But it was their realizations in mathematics and astronomy that were truly breath-taking. While Europe was trying to get through the dark Middle Ages, the Maya calculated the solar year to 365,242 days (which, according to the modern calculations is 365,242198 days) and the moon cycle to 29,5302 days (29,53059 days according to modern calculations). Such staggering calculations could barely have been possible if it weren't for the powerful scale the Maya used.
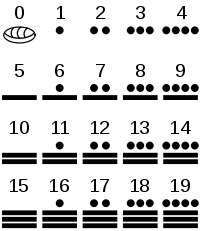
Maya priests and astronomers used a scale with base 20. In that scale, the numbers (0-19) were presented by means of three symbols: zero (form of a shell), one (a dot) and five (a horizontal line). Nineteen (19), for example, is written as four dots that are horizontally next to each other, on top of three horizontal lines that are placed on top of each other. The concepts 'digit' and 'zero' were quite unusual for that time, and completely unknown in Europe.
For Maya numbers consisting of multiple Maya digits— so numbers with a value large than 19 — the Maya numbers are written on top of each other. Here, the number with the highest value is on top. The number thirty-three, for example, is written as a dot (upper Maya number), with three dots underneath, on top of 2 horizontal lines (lower Maya number). The first dot represents "one twenty" or $1 \times 20$, to which three dots and two horizontal lines (13) are added. Consequentially, you get $(1 \times 20) + 13 = 33$. Oddly enough, in the Maya scale the digit in the third position (counted from bottom to top) does not have $20 \times 20 = 400$ as a value, but $18 \times 20 = 360$. Supposedly because 360 is about equal to the number of days in a calendar year. All Maya numbers above the third position (counted from the bottom) again have a normal value according to the 20 digit scale, that makes $360 \times 20 = 7200$ for the fourth digit, $7200 \times 20 = 144000$ for the fifth digit, and so on. This way, the table underneath indicates that $12 \times 360 + 16 \times 20 + 5 = 4645$ and that $9 \times 7200 + 5 \times 360 + 13 \times 20 + 16 = 66876$.
| unit | 33 | 389 | 4645 | 66876 |
|---|---|---|---|---|
| 7200 |
|
|||
| 360 |
|
|
|
|
| 20 |
|
|
|
|
| 1 |
|
|
|
|
Assignment
For this assignment, Maya numbers and Maya digits are represented as strings. The Maya digits with value zero are noted with the letter S, and other digits as a sequence of dots (.; value 1) and hyphens (-; value 5). Here, the dots are always in front of the hyphens. The Maya digits of a Maya number are written next to each other from left to right — separated by a space — instead of on to top of each other. This way, the Maya number with value 66876 is represented as the string "....- - ...-- .---". You are asked to write a function maya2deci that prints the decimal value of a given Maya number. The string representation of this number has to be given to the function as an argument.
Example
>>> maya2deci('..') 2 >>> maya2deci('. ...--') 33 >>> maya2deci('. . ....-') 389 >>> maya2deci('..-- .--- -') 4645 >>> maya2deci('. ..--- ...- ---') 13495 >>> maya2deci('....- - ...-- .---') 66876 >>> maya2deci('...- .-- S S S') 1231200
In het begin van onze jaartelling vestigden de Maya zich in Centraal-Amerika. Ze waren in vele opzichten veruit de meest ontwikkelde en fascinerende beschaving van hun tijd. Wielen en trekdieren waren hen dan wel onbekend, toch beheersten ze als geen ander de kunst van het weven, de architectuur en het pottenbakken. Maar echt adembenemend waren hun verwezenlijkingen op het vlak van wiskunde en sterrenkunde. Terwijl Europa zich door de donkere Middeleeuwen aan het slepen was, berekenden de Maya het zonnejaar op 365,242 dagen (volgens moderne berekeningen 365,242198 dagen) en de maancyclus op 29,5302 dagen (volgens moderne berekening 29,53059 dagen). Zo'n verbluffend accurate berekeningen waren nauwelijks mogelijk geweest zonder het krachtige talstelsel dat de Maya hanteerden.
Mayapriesters en sterrenkundigen gebruikten een talstelsel met basis 20. Daarin worden de cijfers (0-19) voorgesteld aan de hand van drie symbolen: nul (vorm van een schelp), één (een punt) en vijf (een horizontale streep). Zo wordt negentien (19) bijvoorbeeld geschreven als vier punten horizontaal achter elkaar, boven drie horizontale strepen die bovenop elkaar gestapeld worden. De concepten 'cijfer' en 'nul' waren vrij ongebruikelijk voor die tijd, en nog totaal onbekend in Europa.
Voor mayagetallen bestaande uit meerdere mayacijfers — dus getallen met waarde groter dan 19 — worden de mayacijfers verticaal bovenop elkaar geschreven. Hierbij staat het cijfer met de hoogste getalwaarde bovenaan. Het getal drieëndertig wordt bijvoorbeeld geschreven als een punt (bovenste mayacijfer), met daaronder drie punten bovenop 2 horizontale strepen (onderste mayacijfer). Het eerste punt stelt dus "één twintig" of $1 \times 20$ voor, waarbij drie punten en twee horizontale strepen (dus 13) opgeteld worden. Bijgevolg krijg je $(1 \times 20) + 13 = 33$. Vreemd genoeg heeft in het Maya-talstelsel het cijfer op de derde positie (geteld vanaf onder) niet als getalwaarde $20 \times 20 = 400$, maar $18 \times 20 = 360$. Vermoedelijk omdat 360 ongeveer gelijk is aan het aantal dagen in een kalenderjaar. Alle mayacijfers boven de derde positie (geteld vanaf onder) hebben terug een normale getalwaarde volgens het 20-tallig stelsel, dus voor het vierde cijfer $360 \times 20 = 7200$, voor het vijfde cijfer $7200 \times 20 = 144000$, enzoverder. Op die manier geeft onderstaande tabel bijvoorbeeld aan dat $12 \times 360 + 16 \times 20 + 5 = 4645$ en dat $9 \times 7200 + 5 \times 360 + 13 \times 20 + 16 = 66876$.
| eenheid | 33 | 389 | 4645 | 66876 |
|---|---|---|---|---|
| 7200 |
|
|||
| 360 |
|
|
|
|
| 20 |
|
|
|
|
| 1 |
|
|
|
|
Opgave
Bij deze opgave stellen we mayagetallen en mayacijfers voor als strings. Het mayacijfer met waarde nul wordt genoteerd met de letter S, en de andere cijfers als een reeks punten (.; waarde 1) en koppeltekens (-; waarde 5), waarbij de punten altijd voor de koppeltekens staan. De mayacijfers van een mayagetal worden van links naar rechts achter elkaar geschreven — gescheiden door een spatie — in plaats van van boven naar onder. Op die manier wordt het mayagetal met getalwaarde 66876 dus voorgesteld als de string "....- - ...-- .---". Gevraagd wordt om een functie maya2deci te schrijven die de decimale waarde teruggeeft voor een gegeven mayagetal. De stringvoorstelling van dit mayagetal moet als argument aan de functie doorgegeven worden.
Voorbeeld
>>> maya2deci('..') 2 >>> maya2deci('. ...--') 33 >>> maya2deci('. . ....-') 389 >>> maya2deci('..-- .--- -') 4645 >>> maya2deci('. ..--- ...- ---') 13495 >>> maya2deci('....- - ...-- .---') 66876 >>> maya2deci('...- .-- S S S') 1231200
| Added by: | Peter Dawyndt |
| Date: | 2012-09-04 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS