PT07F - A short vacation in Disneyland
After a lot of exams at school, Amber and his friends Ahyangyi, Dragon have a short vacation in Hong Kong Disneyland. Many interesting places they want to visit there: resort, castle,... . In each place and between them, there are special bidirectional rails, so that the visitors can drive a small special car, go around and have a sightseeing tour. This rail system is quite optimal it has tree shape ! Each time, you start a new route (or you can call it "path") with a car, you must purchase a new ticket.
Amber and his friends surely want to visit all places, and each place exactly once, so bored to visit one place many times. But the trouble is they don't carry much money. So Amber thinks about a good way to purchase as small number of tickets as possible (i.e. minimal number of routes). We don't care how they can switch cars during their trip.
Now you're given maps of the Disneyland, please help them to find an optimal solution.
Take a look at the figure below:
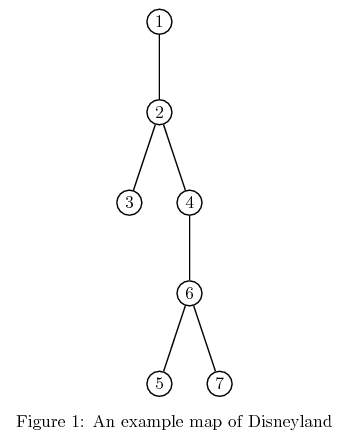
There are many optimal solutions here and Amber must purchase at least 3 tickets, for 3 disjoint routes. Two possible solutions are:
Solution 1:
1-st route: they visit 1 2 3
2-nd route: they visit 4
3-rd route: they visit 5 6 7
Solution 2:
1-st route: they visit 1 2 4 6 5
2-nd route: they visit 3
3-rd route: they visit 7
Input
There may be many maps in one input file. The first line of file is number of maps T (0 < T <= 10). The following line is blank. Then, there are the descriptions of T maps.
For each map, the first line contains one integer N --- number of places in the Disneyland
(0 < N <= 10000). We number places from 1 to N. Next N-1 lines contain N-1 rails between places --- Each line contains a pair (u, v) means
there is a rail between place u and place v (1 <= u,v <= N).
There is a blank line after each description.
Output
For each map, the first line, write minimal number of routes K.
Next K lines, show out the routes in your solution, each has form u[1] u[2]...u[m], means the route starts at
place u[1] then visits place u[2],..., ends at place u[m]. So between 2 consecutive places in each route must have
a rail. If there are many solutions, any of them will be accepted.
There is no blank line after each case.
Example
Input: 1 7 1 2 2 3 2 4 4 6 5 6 6 7 Output: 3 1 2 3 4 5 6 7
hide comments
|
|
abhi123valani:
2020-08-01 08:48:54
In java , i m getting TLE even the solution is of O(n),
|
|
|
arjundabra:
2016-07-01 10:10:38
printing one extra space after each output line gives wa. Be careful. Also I think the author should fix this issue. |
|
|
Sumit Paroothi:
2016-04-15 08:49:29
repeatedly getting wa, any good test cases ?? |
|
|
EsVee:
2015-07-21 23:24:27
Can the author check my solution? |
|
|
xxbloodysantaxx:
2015-07-21 09:02:58
I know that making a route will cause generation of subproblems but yet I cannot think how to define the state!! |
|
|
Sudharsansai:
2015-03-08 10:07:47
Wow....Nice question... |
|
|
wen:
2014-02-19 14:29:35
Please relax the Time Limit of the problem a little bit.
|
|
|
Raghavendran Ramachandran:
2012-09-14 10:47:33
I got 3 WA's because I didn't put a newline after the last test case. |
|
|
Walrus:
2012-08-26 05:52:03
Spent hours before I figured out the leading space problem on my own :-| |
|
|
farzad abdolhoseini:
2012-07-26 12:08:04
isn't there a way to put Mateusz's advice in the problems text?
|
| Added by: | Thanh-Vy Hua |
| Date: | 2007-04-07 |
| Time limit: | 0.100s-1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | Co-author Amber |

 RSS
RSS