TAP2014H - Rush hour
[Due to SPOJ restrictions, this problem has been modified with respect to the original version used in the Argentinian Programming Tournament of 2014 in order to have multiple test cases per input file. http://dc.uba.ar/events/icpc/download/problems/tap2014-problems.pdf ]
Nlogonia is a very organized city, where the houses of the inhabitants are all located on the East End of the city and their workplaces are located on the West End.
Each working day, people go to their workplace in the West and at the end of the day they return to their homes in the East. They rely on the urban rail system of Nlogonia for transportation.
The train company offers N different services. Each of them makes a journey that links a station on the West to a station on the East. There are exactly N stations on the West and N stations on the East. At both ends, the stations are numbered from 1 to N following North-South order. The station furthest to the North is identified with the number 1 and the station furthest to the South with the number N. On both ends, each station belongs to exactly one service.
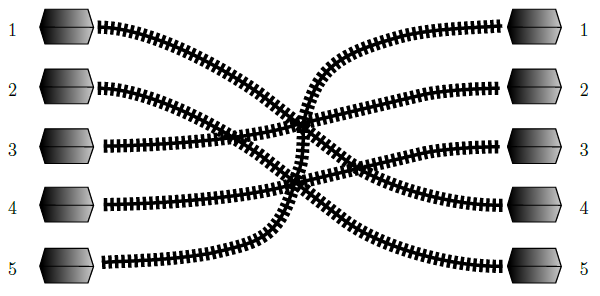
Figure 1: Situation with N = 5 stations corresponding to the first sample input.
When the workday ends, the Nlogonians leave their workplaces eager to return home. This results in heavy traffic over the rail system usually known as "rush hour traffic".
As shown in Figure 1 above, some train services cross over their paths. Two paths cross each other if and only if the relative order of the trains in the North-South direction is different when leaving the West station than when they reach the East station.
To avoid accidents, Nlogonia's train company decided to schedule the trains' departures in shifts so that there are no two trains whose routes cross leaving on the same shift. They want to avoid delays, so their goal is to come up with a schedule such that the number of shifts is minimized. Luckily, there is exactly one train of each service leaving on rush hour.
Continuing with the example of the previously shown Figure 1, the service departing from station 5 intersects with all the other services, therefore a shift must be scheduled exclusively for its departure. The remaining four services cannot be scheduled on a single shift as there are some crossings among them. However, it is possible to group them into two shifts, one for trains leaving stations 1 and 2, and another one for trains leaving stations 3 and 4. Thus, a total of 3 shifts will be necessary to avoid all risk of collissions.
You will be responsible for this task: given the descriptions of the N train services in Nlogonia, you must determine the minimum number of turns in which you can plan train departures avoiding all possible risk of accidents.
Input
The first line contains an integer number T, the number of test cases (1 ≤ T ≤ 200). T test cases follow.
The first line of each test case contains an integer N indicating the number of train services in Nlogonia (1 ≤ N ≤ 105). The second line contains N different integers E1, E2, ..., EN (1 ≤ Ei ≤ N), indicating that the train leaving the i-th station on the West should get to station Ei on the East, for i = 1, 2, ..., N.
Output
For each test case, print a line containing a single integer representing the minimum number of turns in which the services can be planned.
Example
Input: 3 5 4 5 2 3 1 3 1 2 3 9 9 4 2 7 8 3 5 6 1 Output: 3 1 4
hide comments
|
|
SUBHAJIT GORAI:
2015-09-22 22:05:13
learnt something new..... Last edit: 2015-09-24 14:04:05 |
|
|
Fidel Schaposnik:
2014-10-02 01:12:10
@Rahul Jain: Sorry about that, should be correct now, thanks for pointing it out! |
|
|
Nicolás Alvarez:
2014-10-02 01:12:10
@Rahul: You are right, the input description doesn't match. The first number on the input indicates the number of testcases following. We'll fix that when we can. |
|
|
Rahul Jain:
2014-10-02 01:12:10
You didn't mention about testcases.
|
| Added by: | Fidel Schaposnik |
| Date: | 2014-09-29 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Argentinian Programming Tournament 2014 |

 RSS
RSS