TRICENTR - Triangle From Centroid
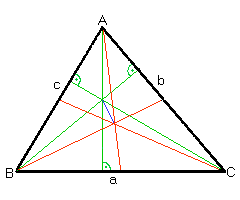
Given the length of side a of a triangle and the distances from the centroid (the point of concurrence of the medians - red in the picture) to all sides: a, b and c, calculate this triangle's area and the distance (blue line) from the orthocenter (the point of concurrence of the heights - green in the picture) to the centroid.
Input
In the first line integer n - the number of test cases (equal to about 1000). The next n lines - 4 floating point values: the length of side a, and distances from the centroid to sides a, b and c.
Output
n lines consisting of 2 floating point values with 3 digits after the decimal point: the area of the triangle and the distance from the orthocenter to centroid.
Example
Input: 2 3.0 0.8660254038 0.8660254038 0.8660254038 657.8256599140 151.6154399062 213.5392629932 139.4878846649 Output: 3.897 0.000 149604.790 150.275
hide comments
|
|
c7h5n3o6_tnt:
2022-05-24 03:17:21
For anyone who want to view my code and give me a helping hand, <snip>
|
|
|
c7h5n3o6_tnt:
2022-05-23 01:59:31
I passed the example given here, but WA when judging.
|
|
|
arn200:
2021-01-13 15:21:16
AC :) using double instead of float helped.. |
|
|
kesarling:
2020-06-02 18:53:05
RE: "distances from the centroid to sides a, b and c" Does that mean the length of the line drawn from the centroid to the midpoint of the sides a, b and c, or does it mean the perpendicular distance of centroid from the 3 sides?
|
|
|
dmachine7:
2020-04-21 16:48:45
how to calculate orthocentre |
|
|
aman_5050:
2020-04-16 17:25:42
The area I am getting for second set of input is 123287 |
|
|
mayankdhyani:
2018-04-09 14:24:21
I am finding difficulty in solving problems , please anyone suggest me what i should do advance my c++ programming skill. Can anyone suggest me the methods of solving the problems form the websites like this?
|
|
|
aadarsh45:
2018-04-04 15:57:25
Use double instead of float |
|
|
akhilb913:
2017-02-27 08:40:02
Finally!! |
|
|
aexpo:
2016-06-25 08:50:01
AC :)
|
| Added by: | Patryk Pomykalski |
| Date: | 2004-05-22 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS PERL6 VB.NET |

 RSS
RSS