| Submit | All submissions | Best solutions | Back to list |
PROG0318 - Polar coordinates |
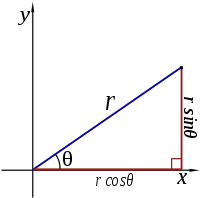
There are two common ways to represent each point of a surface by a pair of co-ordinates: Cartesian co-ordinates and polar co-ordinates. The first coordinate system is the best known. Here, each point is represented by a $x$ and a $y$ co-ordinate. In the second co-ordinate system, each point is represented by a radius $r$ (the distance from the origin), and an angle $\theta$ (the angle between the link to the origin and the positive $X$ axis). Of course there is a connection between these two co-ordinate systems. If a point has the co-ordinates $(x,y)$ and $(r,\theta)$, then the following relationships apply: $$\begin{cases} x = & r \cos(\theta) \\ \\ y= & r\sin(\theta) \end{cases}$$ en $$\begin{cases} r = & \sqrt{x^2+y^2} \\ \\ \theta = & \arctan\left(\frac{y}{x}\right) \end{cases}$$
To solve this exercise you need functions from the math module. These functions are not available by default in a Python program, but you can make them readily available by placing the following line at the head of your code
from math import *
Later we will see a better way to only insert the functions that you need. What functions are available in the math module, can be checked by running the following commands in an interactive Python session:
>>> import math >>> help(math)
Input
The Input consists of two real numbers, each on a separate line, representing respectively the $x$ and $y$ co-ordinate of a given point in the Cartesian co-ordinate system.
Output
The output consists of two real numbers, each on a separate line, respectively the radius $r$ and the angle $\theta$ of the given point, expressed in polar co-ordinates.
Example
Input:
1.0
0.0
Output:
1.0
0.0
Example2
Input:
0.0
3.0
Output:
3.0
1.5707963267948966
Er bestaan twee gangbare manieren om elk punt van een vlak voor te stellen door een paar van coördinaten: cartesische coördinaten en poolcoördinaten. Het eerste coördinatensysteem is het bekendste. Hierin wordt elk punt voorgesteld door een $x$- en een $y$-coördinaat. In het tweede coördinatensysteem wordt elk punt voorgesteld door een straal $r$ (de afstand tot de oorsprong) en een hoek $\theta$ (de hoek tussen de verbinding met de oorsprong en de positieve $X$-as). Natuurlijk bestaat er een verband tussen deze twee coördinatensystemen. Als een punt de coördinaten $(x,y)$ en $(r,\theta)$ heeft, dan gelden de volgende verbanden: $$\begin{cases} x = & r \cos(\theta) \\ \\ y= & r\sin(\theta) \end{cases}$$ en $$\begin{cases} r = & \sqrt{x^2+y^2} \\ \\ \theta = & \arctan\left(\frac{y}{x}\right) \end{cases}$$
Om deze oefening op te lossen heb je functies uit de math module nodig. Deze functies zijn niet standaard beschikbaar in een Python programma, maar je kan ze gemakkelijk beschikbaar maken door de volgende regel bovenaan je programmacode te plaatsen.
from math import *
Later zullen we een betere manier zien om enkel de functies in te voegen die je nodig hebt. Welke functies er allemaal voorhanden zijn in de math module, kan je bekijken door de volgende commando's uit te voeren in een interactieve Pythonsessie:
>>> import math >>> help(math)
Invoer
De invoer bestaat uit twee reële getallen, elk op een afzonderlijke regel, die respectievelijk de $x$- en $y$-coördinaat van een gegeven punt in het cartesisch coördinatensysteem voorstellen.
Uitvoer
De uitvoer bestaat uit twee reële getallen, elk op een afzonderlijke regel, die respectievelijk de straal $r$ en de hoek $\theta$ van het gegeven punt in poolcoördinaten uitdrukken.
Voorbeeld
Invoer:
1.0
0.0
Uitvoer:
1.0
0.0
Voorbeeld
Invoer:
0.0
3.0
Uitvoer:
3.0
1.5707963267948966
| Added by: | Peter Dawyndt |
| Date: | 2013-02-05 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS