Submit All submissions Best solutions PDF Back to list

PROG0385 - N50

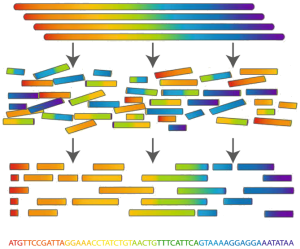
Determining an organism's complete genome (called genome sequencing) forms a central task of bioinformatics. Unfortunately, we still don't possess the microscope technology to zoom into the nucleotide level and determine the sequence of a genome's nucleotides, one at a time. However, researchers can apply chemical methods to generate and identify much smaller snippets of DNA, called reads. After obtaining a large collection of reads from multiple copies of the same genome, the aim is to reconstruct the desired genome from these small pieces of DNA. This process is called genome assembly.

fragment assembly
Genome assembly works by blasting many copies of the same genome into smaller, identifiable reads, which are then used to computationally assemble one copy of the genome.

From a computational perspective, genome assembly is an extremely difficult problem. It becomes even harder, because many of the genomes contain large numbers of identical sequences that are repeated at various locations in the genome. Such repetitions often stretch over thousands of nucleotides, and some are found at thousands of different positions across the genome. This especially occurs in the large genomes of plants and animals. As a result, it is often impossible to reconstruct the complete genome and the assembly process ends with a number of large pieces of the genome which are called contigs in this context.

Assignment

To determine the quality of a genome assembly (for example, when comparing two different assembly algorithms that separately have computed contigs starting from the same set of reads), the N50 statistic is often used.

Suppose we denote the list of lengths of the contigs of a genome assembly as $L$ (this is a list of positive integers), then the N50 statistic can be computed in the following way:

  • create a new list $L'$ that contains $n$ copies of each element $n$ from the original list $L$
  • the N50 statistic equals the median of $L'$

Your task:

  • Write a function median that takes a collection (a list, tuple, set, …) of positive integers. This function must return the median of the elements in the given collection as a floating point number.
  • Write a function extend that takes a collection (a list, tuple, set, …) of positive integers. The function must return a new list containing $n$ copies of each element $n$ in the given collection.
  • Use the functions median and extend to write a function N50. This function takes a collection (a list, tuple, set, …) of positive integers representing the lengths of the contigs of a genome assembly. The function must return the N50 statistic for the given collection of contig lengths.

Median

The median of a list of numbers is the number in the middle if the list is sorted in ascending or descending order. If the list contains an even number of values, the median is determined as the average of the two middle numbers of the sorted list.

Example

>>> contigs = (2, 2, 2, 3, 3, 4, 8, 8)
>>> median(contigs)
3.0
>>> extend(contigs)
[2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8]
>>> N50(contigs)
6.0

Source

  • Miller JR, Koren S, Sutton G (2010). Assembly algorithms for next-generation sequencing data. Genomics 95(6), 315-327.

Het bepalen van het volledige genoom van een organisme (genoomsequenering) is één van de hoekstenen van de bioinformatica. Helaas beschikken we nog steeds niet over microscopische technologie die toelaat om tot op nucleotideniveau in te zoomen en zo de reeks nucleotiden van een genoom één voor één af te lezen. Onderzoekers beschikken echter wel over chemische methoden die kunnen toegepast worden voor het genereren en identificeren van kortere DNA fragmenten. In deze context worden de korte fragmenten reads genoemd. Nadat we een grote collectie van reads geïdentificeerd hebben uit meerdere kopieën van hetzelfde genoom, blijft de uitdaging om het genoom te reconstrueren uit deze korte stukjes DNA. Dit proces wordt genoomassemblage genoemd.

fragment assembly
Genoomassemblage gebeurt door een groot aantal kopieën van hetzelfde genoom op te breken in kleinere, identificeerbare reads, die dan gebruikt worden om het genoom computationeel terug samen te stellen.

Genoomassemblage is computationeel gezien een extreem moeilijk probleem. Het wordt nog moeilijker doordat heel veel genomen een groot aantal identieke sequenties bevatten die op verschillende plaatsen in het genoom herhaald worden. Dergelijke herhalingen zijn vaak duizenden nucleotiden lang en sommige kunnen op duizenden verschillende plaatsen in het genoom voorkomen. Dit komt vooral voor in de grote genomen van planten en dieren. Hierdoor is het vaak niet mogelijk om het volledige genoom te reconstrueren, en eindigt het assemblageproces met een aantal grote stukken van het genoom die in deze context contigs genoemd worden.

Opgave

Om de kwaliteit van een genoomassemblage te bepalen (bijvoorbeeld om twee verschillende assemblage-algoritmen te vergelijken, die elk afzonderlijk contigs bepaald hebben vertrekkend van dezelfde verzameling reads) wordt vaak gebruik gemaakt van de N50 statistiek.

Stel dat we de lijst van lengtes van de contigs van een genoomassemblage aanduiden als $L$ (dit is dus een lijst van natuurlijke getallen), dan kan de N50 statistiek als volgt berekend worden:

  • maak een nieuwe lijst $L'$ die $n$ kopieën bevat van elk element $n$ uit de originele lijst $L$
  • de N50 statistiek is dan gelijk aan de mediaan van $L'$

Gevraagd wordt:

  • Schrijf een functie mediaan waaraan een collectie (een lijst, tuple, verzameling, …) van getallen moet doorgegeven worden. De functie moet de mediaan van deze collectie teruggeven als een floating point getal.
  • Schrijf een functie uitbreiding waaraan een collectie (een lijst, tuple, verzameling, …) van natuurlijke getallen moet doorgegeven worden. De functie moet een nieuwe lijst teruggeven, die $n$ kopieën bevat van elk element $n$ uit de gegeven collectie.
  • Gebruik de functies mediaan en uitbreiding om een functie N50 te schrijven. Aan deze functie moet een collectie (een lijst, tuple, verzameling, …) van natuurlijke getallen doorgegeven worden, die de lengtes van de contigs van een genoomassemblage voorstellen. De functie moet de N50 statistiek voor deze collectie van contiglengtes teruggeven.

Mediaan

De mediaan van een lijst getallen is het getal dat in het midden staat als de lijst oplopend of aflopend gesorteerd wordt. Als de lijst een even aantal getallen bevat, dan wordt de mediaan bepaald als het gemiddelde van de twee middelste getallen van de gesorteerde lijst.

Voorbeeld

>>> contigs = (2, 2, 2, 3, 3, 4, 8, 8)
>>> mediaan(contigs)
3.0
>>> uitbreiding(contigs)
[2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8]
>>> N50(contigs)
6.0

Bronnen

  • Miller JR, Koren S, Sutton G (2010). Assembly algorithms for next-generation sequencing data. Genomics 95(6), 315-327.
Submit solution!
Added by:Peter Dawyndt
Date:2013-06-02
Time limit:10s
Source limit:50000B
Memory limit:1536MB
Cluster: Cube (Intel G860)
Languages:PY_NBC
Resource:None
© Spoj.com. All Rights Reserved. Spoj uses Sphere Engine™ © by Sphere Research Labs.