AE5B1 - Byteantean towns
“Segment is the shortest path connecting two points” — this motto was the main motivation for road designers in the Byteantean Empire. For this reason all roads constructed in the Empire were straight and led across the whole country. At each crossing of two roads Byteanteans planted a town. To avoid misunderstandings, Byteanteans never constructed more than two roads that would intersect at a single point.
The Emperor of Byteantis would now like to divide his country into two provinces, as equal in the sense of the number of towns as possible. One of the roads of the Empire will become the borderline between the provinces. The towns that are located strictly on the borderline will not be under authority of any of the provinces, but only of the Emperor himself. He, therefore, would like to compute, for each road, the absolute value of the difference between the number of towns located on one side of the road and on the other side of the road.
Byteman, the court cartographer, spent many days trying to fulfill the Emperor’s order. Your task is to write a program that will help perform his work.
Input
The first line of the standard input contains an integer n (1 ≤ n ≤ 1 000) denoting the number of roads in the Empire. Each of the following n lines contains a description of a single road — four of integers x1, y1, x2, y2 (−1 000 ≤ x1, y1, x2, y2 ≤ 1 000, points (x1, y1) and (x2, y2) do not coincide) separated by single spaces. Each such quadruple represents a single road that is a straight line passing through points (x1, y1) and (x2, y2). No two roads coincide. No three roads intersect at a single point. We assume that the Empire is so large that all intersections of lines representing roads are located within its boundary.
Output
Your program should write out n lines to the standard output — the answers for all roads from the input (in the same order as in the input). The answer for a road is the absolute value of the difference of numbers of towns at both sides of the road.
Example
For the input data:
4 1 -1 1 10 0 0 1 0 2 0 2 1 4 4 -1 -1
the correct result is:
1 2 3 2
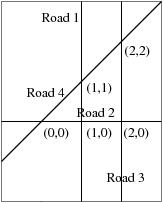
There are five towns in the example, with coordinates (0, 0), (1, 0), (1, 1), (2, 0), and (2, 2).
| Added by: | Race with time |
| Date: | 2009-05-03 |
| Time limit: | 1.539s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | Algorithmic Engagements 2009 |

 RSS
RSS