AVLVKT - Lovely Kitty
Kitty is my sweet sister. Once in a morning I saw she is watching towards the clock. The clock is an analogue clock with two hands. The first one is an hour hand and the other one is a minute hand. While asking about her such attentive mode she replied “Brother can you tell me what will be the angle between the hour hand and the minute hand ?” I was like “huh!!”. Anyway I solved the problem after a while.
Now here is the task for you. I will give you the angle created between the hour hand and the minute hand. You need to find out the how many organizations of hour and minute hands are there that create such angle. For example if I say 90o then the answer will be – 2. The first one is 03:00 and 9:00.
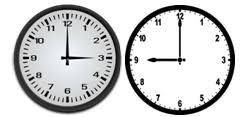
Note that, the angle calculation should be done in clockwise direction but if you figure out an angle greater than 180o then deduct 180o from it. Because kitty do not understand the calculations of angle more than 180o .
Input
Input starts with an integer T that denotes number of test cases. Each of the next T lines contains a real number with one decimal place that denotes angle A.
Constraints
1 <= T <= 2000
1 <= A <= 180.0
Output
For each test case print the case number followed by the result according to the following format Case X: R where X denotes the case number and R denotes the result. See the sample for further clarification.
Example
Input:2
90.0
180.0 Output:Case 1: 2
Case 2: 2
hide comments
|
|
Simes:
2019-12-07 11:01:56
Steps to get AC:
|
|
|
Oleg:
2018-12-01 18:38:13
Problem is mess.
|
|
|
:D:
2018-10-14 16:27:14
I also don't understand what is being asked in this problem. I tried few assumptions, but all seem to be incorrect. How is the clock "ticking" in full minute intervals or seconds? Do hands move fluently? Do the hour hand move with every minute (as on every digital clock) or only on a full hour? How is the angle being measured: from hour hand to minute hand or is minute hand to hour hand also correct. Last edit: 2018-10-14 16:28:05 |
|
|
Prateek chandan:
2018-10-10 12:53:59
Please explain the answer for 180.
|
| Added by: | Avik Sarkar |
| Date: | 2018-07-14 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | Own |

 RSS
RSS