CFRAC2 - Continuous Fractions Again
A simple continuous fraction has the form:
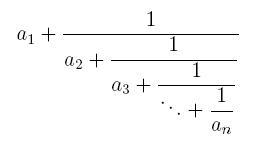
where the ai’s are integer numbers.
The previous continuous fraction could be noted as [a1, a2, ..., an]. It is not difficult to show that any rational number p / q, with integers p > q > 0, can be represented in a unique way by a simple continuous fraction with n terms, such that p / q = [a1, a2, ..., an−1, 1], where n and the ai’s are positive natural numbers.
Now given a simple continuous fraction, your task is to calculate a rational number which the continuous fraction most corresponds to it.
Input
Input for each case will consist of several lines. The first line is two integer m and n, which describe a char matrix, then followed m lines, each line cantain n chars. The char matrix describe a continuous fraction The continuous fraction is described by the following rules:
- Horizontal bars are formed by sequences of dashes '-'.
- The width of each horizontal bar is exactly equal to the width of the denominator under it.
- Blank characters should be printed using periods '.'
- The number on a fraction numerator must be printed center justified. That is, the number of spaces at either side must be same, if possible; in other case, one more space must be added at the right side.
The end of the input is indicated by a line containing 0 0.
Output
Output will consist of a series of cases, each one in a line corresponding to the input case. A line describing a case contains p and q, two integer numbers separated by a space, and you can assume that 10^20 > p > q > 0.
Example
Input: 9 17 ..........1...... 2.+.------------- ............1.... ....4.+.--------- ..............1.. ........1.+.----- ................1 ............5.+.- ................1 5 10 ......1... 1.+.------ .........1 ....11.+.- .........1 0 0 Output: 75 34 13 12
hide comments
|
|
hamza007:
2012-06-23 14:04:27
The continued fractions are also pretty large ... int wont suffice , Unsigned ll is to be used for them too .. This costed be several WAs .. |
|
|
Sangha:
2012-02-02 16:03:34
i am getting WA again and again ........ please mention some test cases !!!!!!! |
|
|
VinyleEm:
2011-01-20 06:49:24
Its possible to get AC just using long longs. So, don't worry about overflows. |
|
|
[Trichromatic] XilinX:
2009-03-21 11:35:52
After solving this problem you may try problem CFRAC & ACFRAC. |
| Added by: | Camilo Andrés Varela León |
| Date: | 2007-01-31 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | HNU Contest |

 RSS
RSS