CH3D - Convex Hull 3D
Bytelandian scientists have developed a brand new method for determining the volume of a person's lungs. The idea is simple: the patient is asked to inhale a sufficiently large number of nanobots, which then transmit their exact 3D-coordinates to an external sensor. Early clinical tests proved rather fun (especially for the scientists who were watching the process of nanobot inhalation), but gave rise to several problems of an algorithmic nature. In other words, nobody had any idea of how the volume of the lungs should be determined afterwards. A lung consists of a large number of disjoint alveoli (which can for our purposes be regarded as little hollows), and inhaled nanobots tend to float around aimlessly within the alveolus they happened to fall into. Whereas it is relatively simple to distinguish between different alveoli, establishing the volume of a single alveolus is a tough task.
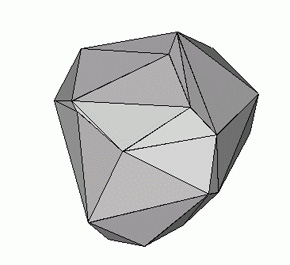
One way to estimate the shape and volume of an alveolus is to smear all nanobots with a little liquid glue and see what they end up stuck to. Another (arguably more humane) method is to calculate the convex hull of the set of points representing nanobot coordinates, its volume and surface area. A convex hull of given set of points in 3D is the convex set of minimum volume which contains all these points.


Input
t – number of test cases [t <= 100], then t tests follow.
Each test starts with integer N - the number of given points [10 <= N <= 1000]. Then exactly N lines follow with 3 real numbers Xi, Yi, Zi in each of them, where [-10.0 <= Xi, Yi, Zi <= 10.0].
Output
For each test case you should output 2 real numbers: the surface area and volume of the hull with precision 0.01.
Example
Input: 1 10 0.00000 0.00000 0.00000 1.00000 0.00000 0.00000 0.00000 1.00000 0.00000 0.00000 0.00000 1.00000 1.00000 1.00000 0.00000 1.00000 0.00000 1.00000 0.00000 1.00000 1.00000 1.00000 1.00000 1.00000 0.50000 0.50000 0.50000 0.66666 0.77777 0.88888 Output: 6.0000 1.0000
| Added by: | Roman Sol |
| Date: | 2005-11-28 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | ZCon 2006 |

 RSS
RSS