CHASE1 - Chase
Chase is a two-person board game. A board consists of squares numbered from 1 to n. For each pair of different squares it is known if they are adjacent to one another or they are not. Each player has a piece at his disposal. At the beginning of a game pieces of players are placed on fixed, distinct squares. In one turn a player can leave his piece on the square it stands or move it to an adjacent square.
A game board has the following properties:
- it contains no triangles, i.e. there are no three distinct squares such that each pair of them is adjacent,
- each square can be reached by each player.
A game consists of many turns. In one turn each player makes a single move. Each turn is started by player A. We say that player A is caught by player B if both pieces stand on the same square. Decide, if for a given initial positions of pieces, player B can catch player A, independently of the moves of his opponent. If so, how many turns player B needs to catch player A if both play optimally (i.e. player A tries to run away as long as he can and player B tries to catch him as quickly as possible).
Example
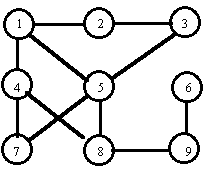
Consider the board in the figure. Adjacent squares (denoted by circles) are connected by edges. If at the beginning of a game pieces of players A and B stand on the squares 9 and 4 respectively, then player B can catch player A in the third turn (if both players move optimally). If game starts with pieces on the squares 8 (player A) and 4 (player B) then player B cannot catch player A (if A plays correctly).
Task
Write a program that for each test case:
- reads the description of a board and numbers of squares on which pieces are placed initially.
- decides if player B can catch player A and if so, computes how many turns he needs (we assume that both players play optimally);
- outputs the result.
Input
The number of test cases t is in the first line of input, then t test cases follow separated by an empty line.
In the first line of a test case there are four integers n, m, a and b separated by single spaces, where 2 <= n <= 3000, n-1 <= m <= 15000, 1 <= a, b <= n. These are (respectively): the number of squares of the board, the number of adjacent (unordered) pairs, the number of the square on which the piece of player A is placed, the number of the square on which the piece of player B is placed. In each of the following lines there are two distinct positive integers separated by a single space, which denote numbers of adjacent squares.
Output
For each test case you should output one line containing:
- one word "No", if player B cannot catch player A, or
- one integer - the number of turns needed by B to catch A (if B can catch A).
Example
Sample input: 1 9 11 9 4 1 2 3 2 1 4 4 7 7 5 5 1 6 9 8 5 9 8 5 3 4 8 Sample output: 3
hide comments
|
|
stef_bart:
2021-08-23 13:37:47
Why is the implementation difficulty of this task rated at 1/50?
|
|
|
kshubham02:
2017-03-15 10:33:46
@devan Yes, he can. |
|
|
devanshukoyalkar:
2015-04-10 19:49:59
Given a chance can A choose not to move? |
| Added by: | Michał Czuczman |
| Date: | 2004-08-10 |
| Time limit: | 5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS PERL6 VB.NET |
| Resource: | 5th Polish Olympiad in Informatics, stage 3 (Adam Borowski) |

 RSS
RSS