CHOCOLA - Chocolate
We are given a bar of chocolate composed of m*n square pieces. One should break the chocolate into single squares. Parts of the chocolate may be broken along the vertical and horizontal lines as indicated by the broken lines in the picture.
A single break of a part of the chocolate along a chosen vertical or horizontal line divides that part into two smaller ones. Each break of a part of the chocolate is charged a cost expressed by a positive integer. This cost does not depend on the size of the part that is being broken but only depends on the line the break goes along. Let us denote the costs of breaking along consecutive vertical lines with x1, x2, ..., xm-1 and along horizontal lines with y1, y2, ..., yn-1.
The cost of breaking the whole bar into single squares is the sum of the successive breaks. One should compute the minimal cost of breaking the whole chocolate into single squares.
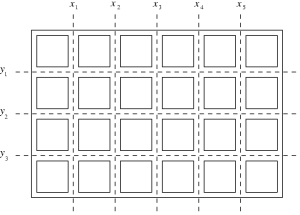
For example, if we break the chocolate presented in the picture first along the horizontal lines, and next each obtained part along vertical lines then the cost of that breaking will be y1+y2+y3+4*(x1+x2+x3+x4+x5).
Task
Write a program that for each test case:
- Reads the numbers x1, x2, ..., xm-1 and y1, y2, ..., yn-1
- Computes the minimal cost of breaking the whole chocolate into single squares, writes the result.
Input
One integer in the first line, stating the number of test cases, followed by a blank line. There will be not more than 20 tests.
For each test case, at the first line there are two positive integers m and n separated by a single space, 2 <= m,n <= 1000. In the successive m-1 lines there are numbers x1, x2, ..., xm-1, one per line, 1 <= xi <= 1000. In the successive n-1 lines there are numbers y1, y2, ..., yn-1, one per line, 1 <= yi <= 1000.
The test cases will be separated by a single blank line.
Output
For each test case : write one integer - the minimal cost of breaking the whole chocolate into single squares.
Example
Input: 1 6 4 2 1 3 1 4 4 1 2 Output: 42
hide comments
|
|
mukulrajput34:
2024-01-24 20:42:34
<snip>
|
|
|
deshiyan:
2022-03-31 17:23:17
For all those PYTHON users, in the testcase loop have an extra input(), there is a blank space between every testcase. |
|
|
gamer4life:
2022-01-15 20:26:16
@pallabtewarry just learn c++ |
|
|
pallabtewary:
2021-11-02 04:29:22
One integer in the first line, stating the number of test cases, followed by a blank line
|
|
|
shubham2912:
2021-10-03 09:42:05
For those getting NZEC in python be sure to take input of empty line in **each** test case |
|
|
iuc_01:
2021-08-29 15:06:24
getting NZEC Runtime error in java
|
|
|
vikash_rishu92:
2021-08-03 06:47:12
giving runtime error in python |
|
|
loser_404:
2021-06-17 06:23:09
For above board optimal way to cut into square is:
|
|
|
myth_:
2021-06-11 15:25:53
Make Sure to decrement the value of both m and n by 1...otherwise, it will give a segmentation error or a wrong answer |
|
|
ayushisriv:
2021-06-10 17:23:58
why its showing runtime error for python |
| Added by: | Thanh-Vy Hua |
| Date: | 2004-12-23 |
| Time limit: | 3s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS PERL6 VB.NET |
| Resource: | 10th Polish Olympiad in Informatics, stage 1 |

 RSS
RSS