CONNECT2 - Connect
Your task is to decide if a specified sequence of moves in the board game Connect ends with a winning move.
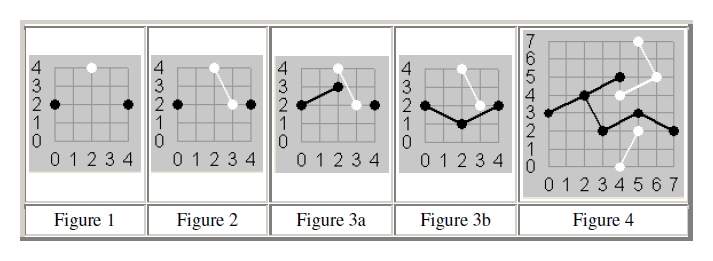
In this version of the game, different board sizes may be specified. Pegs are placed on a board at integer coordinates in the range [0, N]. Players Black and White use pegs of their own color. Black always starts and then alternates with White, placing a peg at one unoccupied position (x, y). Black's endzones are where x equals 0 or N, and White's endzones are where y equals 0 or N. Neither player may place a peg in the other player's endzones. After each play, the latest position is connected by a segment to every position with a peg of the same color that is a chess knight's move away (2 away in one coordinate and 1 away in the other), provided that a new segment will touch no segment already added, except at an endpoint. Play stops after a winning move, which is when a player's segments complete a connected path between the player's endzones.
For example, Figure 1 shows a board with N = 4 after the moves (0,2), (2,4), and (4,2). Figure 2 adds the next move (3,2). Figure 3a shows a poor next move of Black to (2,3). Figure 3b shows an alternate move for Black to (2,1) which would win the game.
Figure 4 shows the board with N = 7 after Black wins in 11 moves:
(0, 3), (6, 5), (3, 2), (5, 7), (7, 2), (4, 4), (5, 3), (5, 2), (4, 5), (4, 0), (2, 4)
Input
The input contains from 1 to 20 datasets followed by a line containing only two zeroes, `0 0'. The first line of each dataset contains the maximum coordinate N (3 < N < 21) and the number of total moves, M (4 < M < 250), with M odd, so Black will always be the last player. The dataset ends with one or more lines each containing two or more coordinate pairs, with a total of M coordinate pairs. All numbers on any line will be separated by blanks. All data will be legal. There will never be a winning move before the last move.
Output
The output contains one line for each data set: `yes' if the last move is a winning move and `no' otherwise.
Example
Input: 4 5 0 2 2 4 4 2 3 2 2 3 4 5 0 2 2 4 4 2 3 2 2 1 7 11 0 3 6 5 3 2 5 7 7 2 4 4 5 3 5 2 4 5 4 0 2 4 0 0 Output: no yes yes
hide comments
|
|
nadstratosfer:
2020-01-07 22:20:24
What an awesome problem! I've never had to deal with the kind of obstacles I encountered here. We need to make a classical version of this one, no discussion! Last edit: 2020-01-08 03:42:33 |
|
|
Simes:
2020-01-05 22:05:28
An interesting problem, should be in classical. |
| Added by: | Nikola P Borisov |
| Date: | 2008-12-04 |
| Time limit: | 0.400s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | ICPC North America Pacific Northwest Region |

 RSS
RSS