CVJETICI - Cvjetici
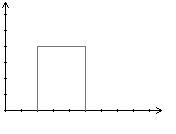
On a faraway planet, strange plants with two stems can be found. Every plant on the planet can be described by three numbers: the x-coordinates of the stems L and R, and the height H at which the stems are connect. The image depicts a plant with L=2, R=5 and H=4.
Every day a new plant grows on the planet. The plant that grows on day 1 is of height 1, and every subsequent plant is one higher than the previous one.
When a stem of a new plant intersects the horizontal segment of another plant, a small flower grows (if one wasn't there already). If segments merely touch in a point, a flower will not grow there. The following images are a visualization of the first example.
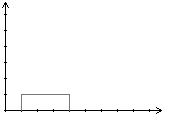
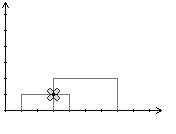
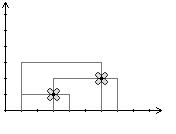
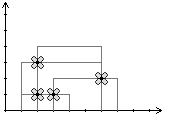
Write a program that, given the coordinates of all plants, calculates the number of new flower every day.
Input
The first line contains an integer N (1 ≤ N ≤ 100 000), the number of days.
Each of the following N lines contains two integers L and R (1 ≤ L < R ≤ 100 000), the coordinates of the stems of a plant.
Output
Output N lines, the number of new flowers after each plant grows.
Example
Input: 4 1 4 3 7 1 6 2 6 Output: 0 1 1 2
Input: 5 1 3 3 5 3 9 2 4 3 8 Output: 0 0 0 3 2
| Added by: | Race with time |
| Date: | 2009-02-17 |
| Time limit: | 0.203s-0.406s |
| Source limit: | 2000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO PERL6 |
| Resource: | COCI 2008/2009 - Croatian Regional |

 RSS
RSS