DANCE - The Gordian Dance
The Gordian Dance is a traditional Bytelandian dance performed by two pairs of dancers. At the beginning the dancers are standing in the corners of the square ABCD, forming two pairs: A-B and C-D. Every pair is holding an outstretched string. So in the starting position both strings are stretched horizontally and parallel.
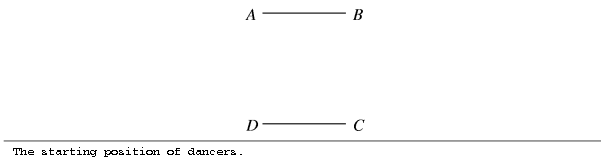
The dance consists of a series of moves. There are two kinds of moves:
- (S) The dancers standing at points B and C swap positions (without releasing their strings) in such a way that the dancer standing at B raises the hand in which he is holding the string and, when going to point C, lets the dancer going from C to B pass in front of him, under his arm.
- (R) All dancers make a turn by 90 degrees clockwise without releasing their strings. This means that the dancer from A goes to B, the dancer from B goes to C, the dancer from C goes to D, and the dancer from D goes to A.
During the dance the strings tangle with each other, but in the end they should be untangled and stretched horizontally and parallel. The dancers do not have to occupy the same spots as in the begining. The dance requires a lot of experience, because the strings can be extremely tangled during the dance. The sequence of moves after which they are no longer tangled and are stretched horizontally and parallel can be difficult to guess.
Your program should help beginner dancers end a dance. You are to determine the minimal number of mover required to end the dance given a sequence of moves already performed.
Illustration
For example after the sequence SS we get the following configuration.
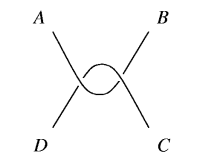
The shortest sequence of moves required to end the dance is of length 5: RSRSS.
Task
Write a program which
- reads from standard input the moves made in a dance,
- finds the minimal number of moves required to untangle the strings and stretch them horizontally and parallel (the dancers don't have to be in their starting spots).
- writes the outcome to standard output.
Input
Ten test cases (given one under another, you have to process all!). The first line of each test case consists of one integer n equal to the nmber of moves already made, 0<=n<=1000000. The second line of each test case consists of one word of length n, made up of letters S and/or R.
Output
For every testcase your program should write to standard output only one line with one integer number: the minimal number of moves required to untangle the strings and stretch them horizontally and parallel.
Example
Input: 2 SS [and 9 test cases more] Output: 5 [and 9 test cases more]Warning: large Input/Output data, be careful with certain languages
hide comments
|
|
(Tjandra Satria Gunawan)(曾毅昆):
2016-04-14 19:16:14
@xqj: to solve it you need 2 identical USB cables, then simulate the problem, find patterns and write algorithm based on that patterns. Seriously, this is how I solve the problem, took ~12 hours for me to sense all the patterns and all "hidden" rules, in the end I came up with two distinct set of rules, but turn out only one of them is accepted :v by the way, this is my first time solving the problem with full pysical experiment only, no mathematical proof needed :p |
|
|
xqj:
2012-04-09 02:02:47
how to sovle it? |
| Added by: | Adam Dzedzej |
| Date: | 2004-06-15 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | Internet Contest Pogromcy Algorytmow(Algorithm Tamers) 2003 Round V |

 RSS
RSS