DEFKIN - Defense of a Kingdom
Theodore implements a new strategy game “Defense of a Kingdom”. On each level a player defends the Kingdom that is represented by a rectangular grid of cells. The player builds crossbow towers in some cells of the grid. The tower defends all the cells in the same row and the same column. No two towers share a row or a column.
The penalty of the position is the number of cells in the largest undefended rectangle. For example, the position shown on the picture has penalty 12.
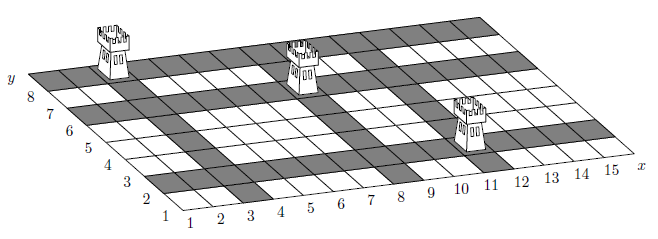
Help Theodore write a program that calculates the penalty of the given position.
Input
The first line of the input file contains the number of test cases.
Each test case consists of a line with three integer numbers: w — width of the grid, h — height of the grid and n — number of crossbow towers (1 ≤ w, h ≤ 40 000; 0 ≤ n ≤ min(w, h)).
Each of the following n lines contains two integer numbers xi and yi — the coordinates of the cell occupied by a tower (1 ≤ xi ≤ w; 1 ≤ yi ≤ h).
Output
For each test case, output a single integer number — the number of cells in the largest rectangle that is not defended by the towers.
Example
Input: 1 15 8 3 3 8 11 2 8 6 Output: 12
hide comments
|
|
gauravg_20:
2023-06-15 14:41:01
push 0,h+1 in height vector and 0,w+1 in width vector before sorting
|
|
|
mafia_987:
2023-03-18 09:56:27
two sortings and just greedy gives accepted. |
|
|
himanshuporwal:
2022-10-03 15:46:36
<snip>
|
|
|
ayush_7901:
2022-07-30 19:32:01
hard to stay simple |
|
|
pathfinder1729:
2021-07-23 23:55:28
cover for n=0!!!!!! |
|
|
charchit099:
2021-07-22 02:56:17
hahaha |
|
|
shr_3:
2021-06-30 07:49:57
complexity would be O(2*Nlog(N)) whare N -> n+2 |
|
|
kshitij_56:
2021-05-25 11:24:34
What is the complexity of this
|
|
|
backtobas:
2020-11-11 16:21:00
I am getting runtime error! |
|
|
akashmodak97:
2020-08-29 10:29:37
Be sure that you're checking about n=0, that cost me one WA :) |
| Added by: | Fidel Schaposnik |
| Date: | 2010-11-08 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | ACM ICPC 2010, NEERC, Northern Subregional Contest |

 RSS
RSS