EQDIV - Equidivisions
An equidivision of an n × n square array of cells is a partition of the n^2 cells in the array in exactly n sets, each one with n contiguous cells. Two cells are contiguous when they have a common side.
A good equidivision is composed of contiguous regions. The figures show a good and a wrong equidivision for a 5×5 square:
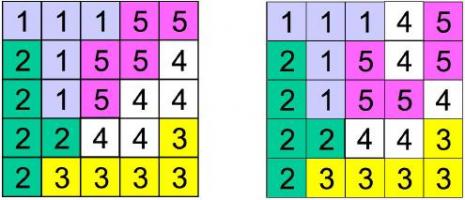
Note that in the second example the cells labeled with 4 describe three non-contiguous regions and cells labeled with 5 describe two non-contiguous regions. You must write a program that evaluates if an equidivision of the cells in a square array is good or not.
Input
It is understood that a cell in an n×n square array is denoted by a pair (i, j), with 1 <= i, j <= n. The input file contains several test cases. Each test case begins with a line indicating n, 0 < n < 100, the side of the square array to be partitioned. Next, there are n − 1 lines, each one corresponding to one partition of the cells of the square, with some non-negative integer numbers.
Consecutive integers in a line are separated with a single blank character. A line of the form
means that cells denoted with the pairs (a1, a2), (a3, a4), ... belong to one of the areas in the partition. The last area in the partition is defined by those cells not mentioned in the n − 1 given lines. If a case begins with n = 0 it means that there are no more cases to analyze.
Output
For each test case good must be printed if the equidivision is good, in other case, wrong must be printed. The answers for the different cases must preserve the order of the input.
Example
Input: 2 1 2 2 1 5 1 1 1 2 1 3 3 2 2 2 2 1 4 2 4 1 5 1 3 1 4 5 5 2 5 3 5 5 5 4 2 5 3 4 3 5 4 3 4 4 5 1 1 1 2 1 3 3 2 2 2 2 1 3 1 4 1 5 1 4 2 4 5 5 2 5 3 5 5 5 4 2 4 1 4 3 5 4 3 4 4 0 Output: wrong good wrong
hide comments
|
|
Rohit Agarwal:
2015-09-08 12:25:56
AC in one go ! :D |
|
|
shikhargarg:
2015-05-14 20:52:37
I m nt getting the input...... can sm1 help me out |
|
|
arbol verde:
2013-03-28 23:28:24
I also used :D comments. If there are extra numbers per line, this shouldn`t be stated in the problem? |
|
|
Vibhor Gaur:
2013-03-24 18:14:47
o(n*n) giving tle hows dat pssible when even taking in the input is o(n*n)
|
|
|
blashyrkh:
2011-09-23 08:35:05
I've discovered that the same cell coordinates may occur more than once in a line. |
|
|
mng:
2011-08-27 20:38:42
Pay attention to :D's comment. It costed me three wrong submissions (including one TLE) before I considered his comment and modified my code to get AC. Thanks :D !!! |
|
|
Santiago Palacio:
2011-06-08 05:22:24
There are no exactly N pairs per colour, that's what :D meant. That's why you should ignore the rest. |
|
|
Santiago Zubieta:
2011-06-04 22:39:20
I'm getting TLE checking if the number of contiguous squares of each color/number does equal or does not equal the N number (if N=5, there must be 5 contiguous square of every color/number...)
|
|
|
Santiago Baldrich:
2011-04-14 01:44:16
There are no extra numbers in the input, read the problem carefully. |
|
|
Ishan:
2011-04-14 01:44:27
should O(n*n) give TLE? |
| Added by: | Camilo Andrés Varela León |
| Date: | 2006-10-25 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | XX Colombian National Programming ACM 2006 |

 RSS
RSS