GCOM - GOOD COMMUNICATION
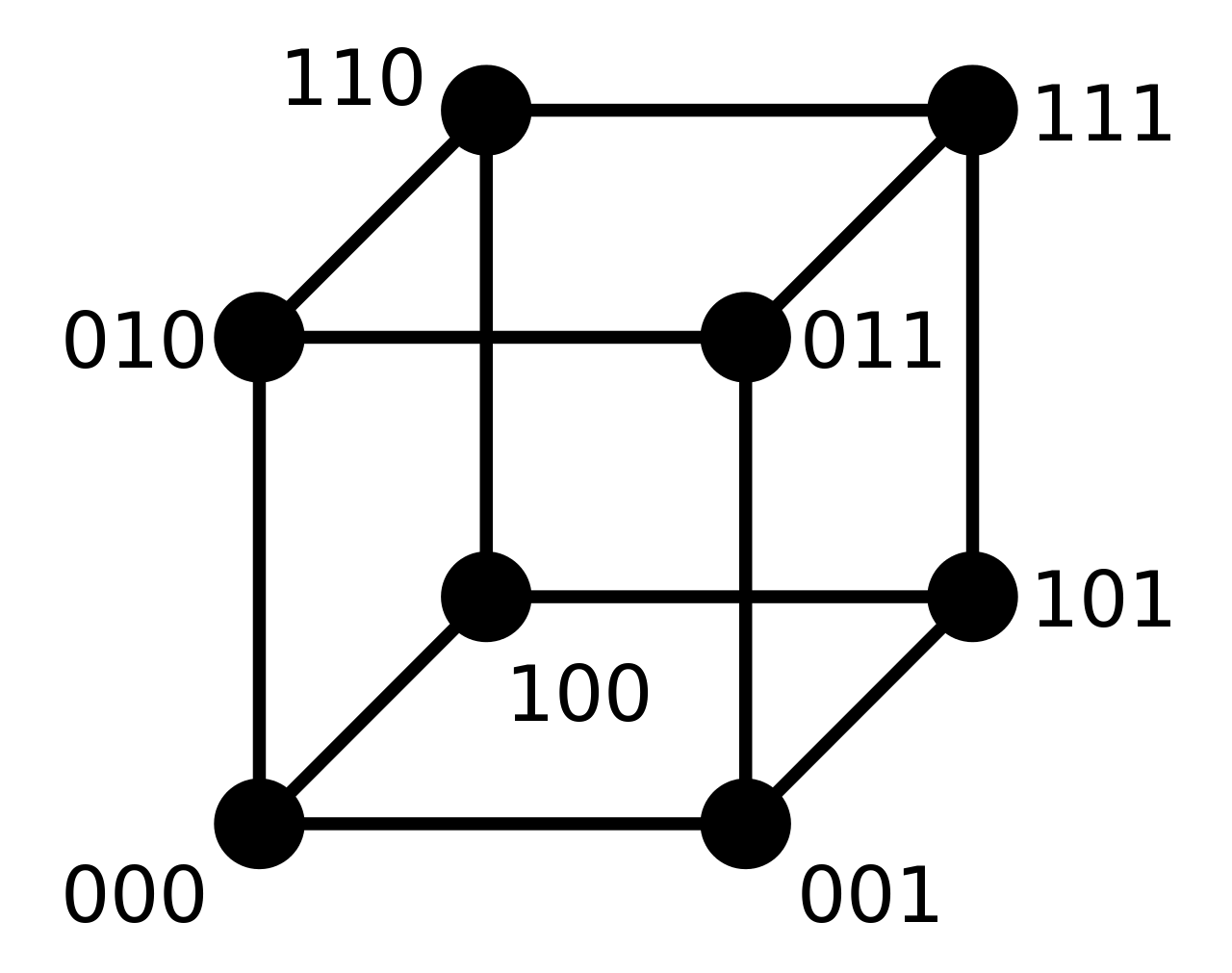
Binary Representation of a number represents a point (vertex) in the N-th dimensional hyper-cube (N is the number of bits used to represent the number in binary form). Eg. point 3 (011) and 5 (101) are shown in 3-dimensional cube in the figure. As the value of points increases, number of axes to represent it in the hyper-cube increases.
Given an N-th dimensional hyper-cube and an array (of size n) of selected points from the cube. We select its complementary point from the cube. We call communication between these points "GOOD" if the distance between given point and its complementary point is maximum. Distance between two points is defined as the bitwise XOR of two points. Let this complementary point be M. The cost of building communication between them is given by
Cost = 2n; where n is position of unset bit which is at farthest distance from MSB in M
To decrease the cost we have two operations:
- Type1: ' q l r ' :- we select two positions l and r from the array. Output the point from the array, between the smaller and larger position being selected, which has minimum cost of building the communication. In case there are multiple answers, print the point with minimum value.
- Type2: ' u x y ' :- update the point at index x with value y.
NOTE:- ' l r x ' are according to 1-based indexing (1 <= l, r, x <= n)
Constraints
1 <= T <= 20
1 <= n, q <= 105
1 <= array elements <= 109
Input
First line contains number of test cases. Next line contains n and q representing size of array and number of operations. Next line contains array elements. Next q lines operations of type1 and type2 in the specified format.
Output
Give answer of the required type in new lines.
Example
Input: 1 3 3 2 3 4 q 1 3 u 2 5 q 1 2 Output: 3 5
hide comments
|
|
anjali_28:
2021-05-08 19:03:03
https://www.spoj.com/submit/GCOM/id=27851333
|
|
|
mehmetin:
2019-12-31 06:24:43
Optimized cin/cout gets time limit, scanf/printf gets acccepted. |
|
|
bdezso:
2019-12-23 09:34:43
@y17prashant
|
|
|
stunner2k18:
2019-12-23 05:09:17
AC in one go!!
|
|
|
y17prashant:
2019-12-20 19:54:31
I have added the image link you can view it from there . |
|
|
bdezso:
2019-12-20 18:03:01
Could you check my last submission?
|
|
|
nadstratosfer:
2019-12-20 11:06:44
Please use https://www.spoj.com/uploads/ for images so that their visibility does not depend on 3rd party servers.
|
| Added by: | 17 Prashant_Singh |
| Date: | 2019-12-16 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |

 RSS
RSS