GNY07H - Tiling a Grid With Dominoes
We wish to tile a grid 4 units high and N units long with rectangles (dominoes) 2 units by one unit (in either orientation). For example, the figure shows the five different ways that a grid 4 units high and 2 units wide may be tiled.
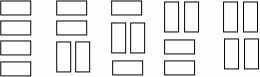
Write a program that takes as input the width, W, of the grid and outputs the number of different ways to tile a 4-by-W grid.
Input
The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the number of datasets that follow.
Each dataset contains a single decimal integer, the width, W, of the grid for this problem instance.
Output
For each problem instance, there is one line of output: The problem instance number as a decimal integer (start counting at one), a single space and the number of tilings of a 4-by-W grid. The values of W will be chosen so the count will fit in a 32-bit integer.
Example
Input: 3 2 3 7 Output: 1 5 2 11 3 781
hide comments
|
|
sleepntsheep:
2023-04-16 05:03:20
Can be solved with plug dp |
|
|
sanskar_native:
2021-05-28 20:16:32
Can be solved using dp with bitmask...see William Fiset's YouTube channels for "Tilling Problem" explanation :) |
|
|
distructo:
2020-12-28 09:59:59
https://www.spoj.com/problems/M3TILE/
|
|
|
sharjeel_spoj:
2020-10-01 21:10:50
Why is it tagged #bitmasks? Can somebody point how to solve with bitmasks?
|
|
|
zakir068:
2020-03-30 08:27:09
for w=0 ans = 1
|
|
|
lnxdx:
2019-10-04 15:23:36
Two ACs in two goes :/ |
|
|
lnxdx:
2018-11-23 17:31:55
The values of W will be chosen so the count will fit in a 32-bit integer.
|
|
|
ushould_study:
2018-09-13 15:07:12
how to define the size of w ? Is there any upper limit to it?
|
|
|
ayusofayush:
2018-08-17 15:51:36
http://journeywithdp.blogspot.com/2018/07/way-to-solve-tiling-problems.html
|
|
|
karan_yadav:
2018-08-05 13:42:00
Before solving this problem solve (https://www.spoj.com/problems/M3TILE/) Last edit: 2018-08-05 13:42:13 |
| Added by: | Marco Gallotta |
| Date: | 2008-03-12 |
| Time limit: | 9.600s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | ACM Greater New York Regionals 2007 |

 RSS
RSS