GNY07H - Tiling a Grid With Dominoes
We wish to tile a grid 4 units high and N units long with rectangles (dominoes) 2 units by one unit (in either orientation). For example, the figure shows the five different ways that a grid 4 units high and 2 units wide may be tiled.
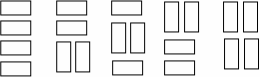
Write a program that takes as input the width, W, of the grid and outputs the number of different ways to tile a 4-by-W grid.
Input
The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the number of datasets that follow.
Each dataset contains a single decimal integer, the width, W, of the grid for this problem instance.
Output
For each problem instance, there is one line of output: The problem instance number as a decimal integer (start counting at one), a single space and the number of tilings of a 4-by-W grid. The values of W will be chosen so the count will fit in a 32-bit integer.
Example
Input: 3 2 3 7 Output: 1 5 2 11 3 781
hide comments
|
|
xxbloodysantaxx:
2015-07-09 21:59:36
No Image found ! Link broken |
|
|
Rishabh Joshi:
2015-03-15 06:58:15
Very nice problem!! Learnt a lot! (hint: how can you start the series? Write all combinations of dominos by which you can start(and continue), and the answer will start to present itself)! |
|
|
Govind Lahoti:
2015-02-13 08:45:32
Awesome problem. Enjoyed solving it :) |
|
|
mayank:
2014-12-18 11:21:07
Tried after M3TILE. Almost similar. Could not get it straight though! :P |
|
|
fanatique:
2014-07-01 19:25:33
good one :) |
|
|
Ravi Shankar Mondal:
2014-06-24 21:34:24
100th green light :) |
|
|
Noob:
2014-05-26 17:18:19
Good one! |
|
|
Himanshu:
2014-01-30 06:33:30
Shouldn't input 3 give 5 + 2*5 - 1 = 14 as each tiling (except last) for input 2 can be widened by adding a column to the left or to the right. |
|
|
Ankit Kumar:
2013-12-30 07:51:38
my 50th on SPOJ :) |
|
|
Hitman:
2013-12-23 21:29:38
for n=0 ans=1 |
| Added by: | Marco Gallotta |
| Date: | 2008-03-12 |
| Time limit: | 9.600s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | ACM Greater New York Regionals 2007 |

 RSS
RSS