GOODA - Good Travels
It's that time of year again - the best ACM-ICPC team of all time is off to the World Finals! Being the best, they realize that a good performance starts before the contest itself - in order to get into the perfect mindset, they must have as much fun on the trip to the contest site as possible!
The Team is interested in a network of N (2 <= N <= 10^6) cities (conveniently numbered 1..N), interconnected by M (1 <= M <= 10^6) one-way flights (similarly numbered 1..M). Their hometown is city S (1 <= S <= N), and the contest will take place in city E (1 <= E <= N, S != E). Flight i goes from city ai (1 <= ai <= N) to city bi (1 <= bi <= N, ai != bi), and no two flights connect the same pair of cities in the same direction. In general, no cities are guaranteed to be reachable from other cities by a sequence of flights. However, The Team of course knows that city E is reachable from city S - they're not about to break their streak of triumphant wins!
Now, each city i has a fun value, fi (0 <= fi <= 10^6), associated with it. Along their trip, The Team will take time to have fun at every city they visit, including the first and last. However, though they can visit a city multiple times (including cities S and E), or even take a certain flight multiple times, surely this gets boring quickly - therefore, any city's fun can only be had up to once.
The Team wants to determine the maximal amount of fun they can have on any sequence of flights that starts at city S and ends at city E. Naturally, every member on The Team is so intelligent that they've calculated this value in their heads (and are quite excited about it) - but can you?
Input
First line: 4 integers, N, M, S, and E
Next N lines: 1 integer, fi, for i = 1..N
Next M lines: 2 integers, ai and bi, for i = 1..M
Output
1 integer, the maximal amount of fun The Team can have on their trip.
Example
Input: 5 6 1 4 5 4 5 10 2 1 2 1 3 2 4 3 4 4 5 5 4 Output: 22
Explanation of Sample
The network of cities and flights looks like this (the fun values of cities are shown below them):
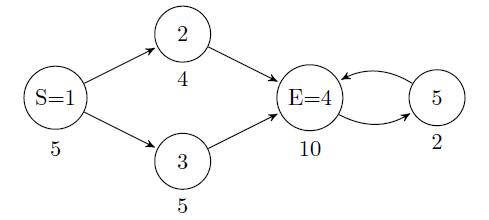
The optimal route that The Team can take goes through cities 1 → 3 → 4 → 5 → 4, yielding a total fun value of 5 + 5 + 10 + 2 + 0 = 22.
hide comments
|
|
RAJDEEP GUPTA:
2013-05-14 11:46:03
Could you please give me a test case for which my solution got SIGSEGV ? If you do not think that it would be a spoiler.
|
| Added by: | SourSpinach |
| Date: | 2013-05-09 |
| Time limit: | 4s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Own problem |

 RSS
RSS