GRAFFDEF - King Graffs Defense
King Graff, the ruler of the land of Feerie, has a problem - his nation is under attack! Luckily, he has an army at his disposal, composed of a whopping $S$ soldiers (where $S = 2$).
Feerie consists of $N$ ($1 \leq N \leq 100,000$) towns (numbered $1..N$), and $M$ ($1 \leq M \leq 500,000$) roads. The $i$th road runs between distinct towns $A_i$ and $B_i$, in both directions. No pair of towns is directly connected by more than one road, but every pair of towns is connected by at least one path of connected roads. King Graff would like to position his two soldiers in two different towns to prepare for the impending assault - however, since he's not much of a strategist, he'll choose the towns at complete random.
Graff's only real concern is with his enemies using a divide-and-conquer strategy. His soldiers will be susceptible to this type of attack if there exists any single road that, if blocked, will prevent them from reaching each other by any system of connected roads. As the royal computer scientist, your job is to determine the probability that King Graff will be defeated.
Input
First line: 2 integers, $N$ and $M$
Next $M$ lines: 2 integers, $A_i$ and $B_i$, for $i = 1..M$
Output
1 real number (rounded to 5 decimal places), the probability that the two towns chosen by Graff can be disconnected by the removal of any single road
Example
Input: 4 4 1 2 1 3 2 4 4 1 Output: 0.50000
Explanation of Sample:
The map of Feerie is illustrated below:
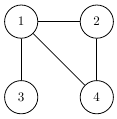
King Graff can make 6 possible choices as to where to place his soldiers, and three of those (the three with one of the soldiers being at town 3) result in defeat (if the road between towns 1 and 3 is destroyed). The probability of failure is then $3/6 = 0.5$.
hide comments
|
|
edith_1111:
2022-07-06 08:35:03
<snip>
|
|
|
karelisp:
2021-04-30 22:59:19
?! SPOILER ?! <snip>
|
|
|
kesh4281:
2020-03-28 06:28:41
extra digits in output wont give u wrong. and constraints seems to be right N<=100000 and there is no case with N=1
|
|
|
Bojan Rosko:
2018-10-09 11:21:04
Watch for integers overflow, I had a stupid bug where I calculated number of all combinations as
|
|
|
im_loving_it:
2018-08-28 09:03:03
constraint & test data are correct :p Last edit: 2018-11-25 11:02:56 |
|
|
ashishgup:
2018-07-25 15:59:42
Constraints for N are wrong :/
|
|
|
nidhi_061:
2018-06-16 07:39:48
someone, please provide more test cases. |
|
|
[Rampage] Blue.Mary:
2016-01-26 10:34:21
There won't be any test case with N=1. |
| Added by: | SourSpinach |
| Date: | 2013-05-12 |
| Time limit: | 2s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Own problem |

 RSS
RSS