GRAFFTRI - King Graffs Trip
King Graff, the ruler of the land of Feerie, is going on a trip through his realm! He would like to give his people a chance to see their great king amongst them, almost as if he too were a petty commoner with no future.
Feerie consists of $N$ ($1 \leq N \leq 10^4$) towns (numbered $1..N$), and $M$ ($1 \leq M \leq 10^5$) roads. The $i$th road runs from town $A_i$ to a different town $B_i$ (and can only be travelled in that one direction), and takes $T_i$ ($1 \leq T_i \leq 10^9$) minutes to traverse. No pair of towns is directly connected by more than one road in the same direction. King Graff will start his trip at town $X$, and would like to end at a different town $Y$. Furthermore, since he has better things to do, he would like to complete it in at most $L$ ($1 \leq L \leq 10^{15}$) minutes.
However, Graff does not like to go long without being worshipped, and the only proper place to do this is in a shrine built to him. $S$ ($1 \leq S \leq 100$) distinct towns contain such shrines - the $i$th shrine is in town $H_i$. He would like to minimize the longest continuous stretch of time spent during the trip without passing through any shrines. As the royal computer scientist, your job is to determine the length of this stretch, or break the news to your king that the trip cannot be completed in time. Note that the trip may be impossible to complete in any amount of time, if town $Y$ is not reachable from town $X$ by any path of connected roads.
Input
First line: 5 integers, $N$, $M$, $X$, $Y$, and $L$
Next $M$ lines: 3 integers, $A_i$, $B_i$, and $T_i$, for $i = 1..M$
Next line: 1 integer, $S$
Next $S$ lines: 1 integer, $H_i$, for $i = 1..S$
Output
Line 1: 1 integer - the minimum value for the longest continuous stretch of travel time spent away from shrines (in minutes), or -1 if the trip cannot be completed in at most $L$ minutes
Example
Input: 5 7 2 3 7 2 3 5 3 2 1 2 1 4 1 3 3 2 4 3 4 5 2 5 3 3 3 1 4 5 Output: 4
Explanation of Sample:
The map of Feerie is illustrated below:
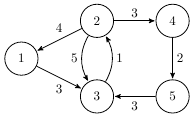
The optimal route goes through towns $2 \rightarrow 1 \rightarrow 3$, taking 7 minutes with at most 4 minutes spent away from any shrines. The route $2 \rightarrow 3$ is shorter (taking 5 minutes), but has a longer continuous time away from shrines (5). The route $2 \rightarrow 4 \rightarrow 5 \rightarrow 3$ has a shorter such value (3), but takes longer than 7 minutes in total (8) and as such is not allowed.
hide comments
|
|
mehmetin:
2019-01-09 17:10:45
The problem description for this problem - and maybe others in the series - should be reformatted. Lots of unformatted text in the description, that makes it difficult to read (I opened the page on Chrome and Firefox on Linux, maybe it's different with other systems, like Windows or MacOs) |
|
|
hodobox:
2016-06-23 05:14:18
Blue.Mary is ridiculous. Rishav Goyal is fine.
|
|
|
[Rampage] Blue.Mary:
2016-01-27 04:03:52
Rishav Goyal is ridiculous. The problem description is fine. |
|
|
Rishav Goyal:
2015-08-11 08:22:44
problem description is ridiculous |
|
|
Anirban Saha:
2013-06-15 10:45:32
@Jacob I cannot get why I am getting wa. Can you please check submission id 9483233 and provide a test case. |
| Added by: | SourSpinach |
| Date: | 2013-05-12 |
| Time limit: | 2s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Own problem |

 RSS
RSS