HEXAGON - Hexagon
Consider a game board consisting of 19 hexagonal fields, as shown in the figure below. We can easily distinguish three main directions in the shape of the board: from top to bottom, from top-left to bottom-right, and from top-right to bottom-left. For each of these primary directions, the board can be viewed as a series of rows, consisting of 3, 4, 5, 4, and 3 fields, respectively.
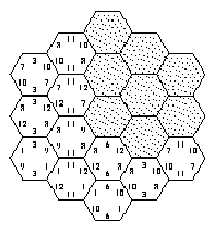
The game board has to be completely covered using a set of hexagonal pieces. Each piece carries three numbers, one for every primary board direction. Only three different numbers are used for each direction. Every possible combination of three numbers for all three directions is assigned to a piece, leading to a set of 27 unique pieces. (The board in the above figure is still in the process of being covered.)
The score of a board is calculated as the sum of all 15 row scores (5 rows for each primary direction). The row scores are calculated as follows: if all pieces in a row carry the same number for the direction of the row, the row score is this number multiplied by the number of pieces in the row. Otherwise (the pieces carry different numbers in the row direction) the row score is zero. Note that the pieces may not be rotated. For example, the score of the leftmost row in the figure is 3 . 3 = 9, the score of the row to its right is 4 . 11 = 44.
While in the real game the pieces are chosen randomly and the set of pieces is fixed, we are interested in the highest possible score for a given set of numbers for each direction, when all pieces in a row carry the same number for the direction of the row. This means you have to choose those 19 pieces that result in the highest score under the constraint that each row has a score greater than zero.
Input
The first line of the input file contains an integer n which indicates the number of test cases. Each test case consists of three lines containing three different positive integers each. Each of these three lines contains the numbers for a single primary direction. From these numbers the set of pieces is generated.
Output
For each test case output a line containing the number of the case ("Test #1", "Test #2", etc.), followed by a line containing the highest possible score for the given numbers. Add a blank line after each test case.
Example
Input: 1 9 4 3 8 5 2 7 6 1 Output: Test #1 308
hide comments
|
|
hodobox:
2020-06-25 14:00:56
Ignore the other comments, you can write a fancy algorithm and it will work just fine :) |
|
|
:D:
2010-10-07 13:05:12
Yes, this is one of those problems where a statesment can be a little hard. You also shouldn't look for any fancy algorithms. Somewhat straight foward approach will be enogth. |
|
|
.::Manish Kumar::.:
2010-10-07 13:05:12
Guys , this is a easy question....(since excluding I/O ...exactly 3 lines)...give it a try! Last edit: 2010-09-28 17:00:23 |
|
|
Adrian Kuegel:
2010-10-07 13:05:12
You can use each of the 27 pieces at most once! Try to get the score of 312 obeying this constraint, and you will see it is impossible. |
|
|
Subodh Kumar Singh:
2010-10-07 13:05:12
How is 312 wrong, i dint get it yet ! Please someone explain. |
|
|
Adrian Kuegel:
2010-10-07 13:05:12
Show me an arrangement with this score and which uses each of the 27 pieces at most once. |
|
|
P != NP:
2010-10-07 13:05:12
i dont get the question.
|
| Added by: | Adrian Kuegel |
| Date: | 2005-07-04 |
| Time limit: | 13.33s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: OBJC |
| Resource: | ACM Southwestern European Regional Contest 1996 |

 RSS
RSS