IITKESO207PA6Q1 - Strongly Connected Components
Given a digraph G = (V, E), print the strongly connected component graph GSCC = (VSCC, ESCC).
Labeling of vertices in VSCC should be done as follows:
For vertex v in VSCC , let us define order-id(v) = min{label(vi) | vi is part of v in VSCC}
Vertex v in VSCC with lowest value of order-id(v) gets label 0, vertex with second lowest value gets label 1 and so on.
Input
The graph is given in the adjacency list format. The first number is n, the number of vertices, which will be an integer ≥ 1. The vertex set is assumed to be V = {0, 1, . . . , n − 1}. Following this number n, there are n lines, where, the ith line (1st , 2nd ...) corresponds to the adjacency list of node numbered i-1 (0,1,...). Each adjacency list is a sequence of vertex ids (between 0 and n − 1) and ends with -1.
Output
Print the number of strongly connected components.
From the next line , print the sorted adjacency list of each SCC appended with -1
Constraints
2 <= n <= 1000
TIme - 1s
Example 1:
Input:
9
1 -1
4 3 2 -1
5 -1
-1
0 -1
6 -1
7 -1
8 -1
2 -1
Output:
3
1 2 -1
-1
-1
Explanation:
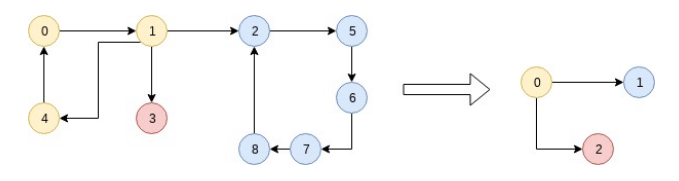
In the above example, there will be 3 SCCs : {0, 1, 4}, {2, 5, 6, 7, 8} and {3}.
SCCs of {0, 1, 4}, {2, 5, 6, 7, 8}, {3} have order-ids 0, 2 and 3 respectively. Therefore, {0, 1, 4} gets label 0, {2, 5, 6, 7, 8} gets label 1 and {3} gets label 2. There are two edges (0, 1) and (0, 2) in the condensed graph GSCC. Verify the same in the following diagram:
Example 2:
Input:
10
1 -1
9 -1
4 5 7 9 -1
4 -1
-1
4 -1
1 8 -1
-1
-1
1 -1
Output:
9
1 -1
-1
1 4 5 7 -1
4 -1
-1
4 -1
1 8 -1
-1
-1
| Added by: | ESO207 IITK |
| Date: | 2018-04-08 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |

 RSS
RSS