INTSS - Internally Stable Sets
A weighted finite undirected graph is a triple G = (V, E, w) consisting of vertex set V, edge set 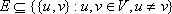 , and vertex weighting function w such that
, and vertex weighting function w such that 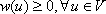 and
and 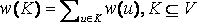 . For
. For 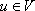 and
and 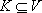 , N(u) and N(K) will denote the neighboring vertex sets of u and K respectively, formally defined as:
, N(u) and N(K) will denote the neighboring vertex sets of u and K respectively, formally defined as:

A vertex set 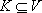 satisfying
satisfying 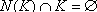 is called internally stable (also known as independent or anti-clique). In this problem you must find an internally stable set B such that w(B) = max{w(S)}, where S belongs to the set of all internally stable sets of that graph.
is called internally stable (also known as independent or anti-clique). In this problem you must find an internally stable set B such that w(B) = max{w(S)}, where S belongs to the set of all internally stable sets of that graph.
Input
t – the number of test cases [t <= 100]
n k – [n – number of vertices (2 <= n <= 200), k – number of edges (1 <= k <= n*(n-1)/2)]
then n numbers follows (wi - the weight of i-th vertex) [ 0 <= wi <= 2^31-1]
then k pairs of numbers follows denoting the edge between the vertices (si sj edge between i-th and j-th verices) [1 <= si, sj <= n]
Output
For each test case output MaxWeight – the weight of a maximum internally stable set of the given graph. [ 0 <= MaxWeight <= 2^31-1]
Example
Input: 2 5 6 10 20 30 40 50 1 2 1 5 2 3 3 4 3 5 4 5 4 4 10 4 10 14 1 2 2 3 3 4 4 1 Output: 70 20
hide comments
|
|
gautams:
2015-07-17 06:41:32
I have solved the problem but it is exceeding time limit. Please help. Do I have to know any specific thing in graph theory ?? |
|
|
Alex:
2013-01-02 18:52:01
Isn't this an NP-hard problem? |
|
|
Leonardo Lopez:
2012-10-02 19:17:44
This is a tutorial exercise? |
|
|
[Trichromatic] XilinX:
2009-04-13 03:07:17
Hard versions of this problem are MIS & MAXISET (Actually, both these two codes mean "Maximum Independent Set" :-) |
| Added by: | Roman Sol |
| Date: | 2004-12-14 |
| Time limit: | 21s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | ZCon |

 RSS
RSS