KTRANS - K-transfer journey
There are N cities numbered from 1 to N, connected by M flights. Note that a flight from city 1 to 2 doesn't necessarily mean there is a flight from 2 to 1, and some cities may not be connected by any flights. Also, there is at most one directed flight from one city to another one. The i-th flight connects city Ui with city Vi, takes Wi seconds, plus a constraint: the current accumulated travel time cannot exceed Li when you are in Ui and plan to go to Vi from there for health reason.
Duck wants to travel, but he will be very tired if he takes too many flights! Therefore, he doesn't want to take more than K flights. Can you find out the shortest travel time for all pairs of cities by not taking more than K flights and following the accumulated travel time constraint of each flight?
Input
The first line is the number of test cases T. (1 ≤ T ≤ 20)
For each test case, it starts with N, M, K. (2 ≤ N ≤ 50, 0 ≤ M ≤ N × (N - 1), 1 ≤ K ≤ N - 1)
Following M lines, each consisting Ui, Vi, Wi, Li. (1 ≤ Ui, Vi ≤ N where Ui ≠ Vi, 1 ≤ Wi ≤ 104, 1 ≤ Li ≤ 104 × 50)
Output
Output a N × N distance matrix, printing out the shortest travel time for all pairs of cities. If one city is not reachable from one city, print out -1 instead.
Example
Input: 2 8 15 3 1 2 4 10 1 7 7 28 1 8 4 27 2 3 9 34 2 6 6 14 2 7 8 7 2 8 1 12 3 5 10 24 5 3 8 39 5 4 6 28 5 6 5 11 6 5 6 9 7 2 4 6 7 6 7 12 8 3 3 3 6 9 5 1 2 10 31 1 3 14 58 1 5 23 24 3 1 12 12 3 2 4 19 4 1 20 53 4 5 25 47 5 4 13 47 6 2 4 39 Output: 0 4 13 -1 23 10 7 4 -1 0 4 18 12 6 8 1 -1 -1 0 16 10 15 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 8 6 0 5 -1 -1 -1 -1 14 12 6 0 -1 -1 -1 4 13 19 13 7 0 5 -1 -1 3 19 13 -1 -1 0 0 10 14 36 23 -1 -1 0 -1 -1 -1 -1 12 4 0 48 35 -1 20 30 34 0 25 -1 33 -1 47 13 0 -1 -1 4 -1 -1 -1 0
Explanation
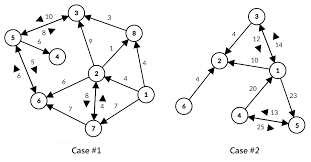
Select some results to explain, won't go through all..
In case 1, 1 → 3 is 13 through 2, rather than 7 through 8 because 1 → 8 is 4, and 8 to 3 has a accumulated time constraint which is 3.
8 → 6 is not reachable although there is exactly one path connecting them and within K, the constraint of 5 → 6 is 11, which is larger than accumulated time of 13.
In case 2, 5 → 2 is not reachable. Only one path connecting 5 to 1 which takes 33. From 1 → 2 the shortest time is 10 but its constraint is 31 which is larger than 33. So we pass through 3 instead and the total time becomes 47. Unluckily the constraint of 3 → 2 also limits the reachability.
hide comments
|
|
:D:
2019-11-22 14:48:39
Very good problem and the description is well written except for one sentence: "current accumulated travel time cannot exceed Li if you go to Vi from Ui". This reads as if the limit is for accumulated travel time after getting to Vi not right before using the specific connection. Explanations at the bottom clear this out, but it would still be good to correct.
|
| Added by: | him0727 |
| Date: | 2019-11-02 |
| Time limit: | 0.400s-1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | Own problem |

 RSS
RSS