MKLABELS - Making Labels
Trees comes in many varieties other than the popular binary tree. In general, a tree is a connected acyclic graph. That is, it consists of some number of vertices N (which we’ll assume is at least one in this problem), and N – 1 edges, each of which connects a pair of vertices.
A “labeled tree” is a tree in which each vertex has been given a “label.” For simplicity, let us assume these labels are the integers 1 through N. In how many different ways may a tree with N vertices be labeled? By “different” we mean that no rearrangement of two trees with the same number of vertices with different labeling will be identical. (Note that although we commonly associate data with each vertex, and identify one vertex as the root of the tree, that’s not significant in this problem.)
Let’s consider some examples. The figure below shows all possible arrangements of trees with N = 1, 2, 3, 4, or 5 vertices. The number shown below each tree is the number of different ways in which the vertices in each tree can be labeled.
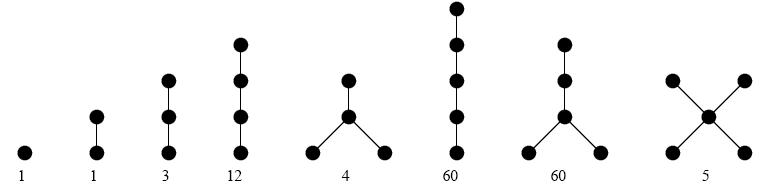
Clearly a tree with only one vertex can be labeled in only one way – by assigning the label “1” to the single vertex. A tree with two vertices can also be labeled in only one way. For example, although the two trees shown on the left below appear to be different, the first can be easily transformed into the second. (Imagine the edges are strings, so the vertices can be easily repositioned without losing their connectivity.)

There are, however, three possible ways to label the vertices in a 3-vertex tree, as shown on the right above. No matter how you rearrange the labeled vertices in any of the three trees, you cannot produce any of the other labeled trees.
In a similar manner, the various arrangements of four vertices in a tree yield a total of 16 possible labelings – 12 for the four vertices “in a row,” and 4 for the other configuration. There are three possible arrangements of the vertices in a tree with N = 5, with a total of 125 possible
Input
There will be multiple cases to consider. The input for each case is an integer N specifying the number of vertices in a tree, which will always be between 1 and 10. The last case will be followed by a zero.
Output
For each input case, display the case number (1, 2, …), the input value of N, and the number of different ways in which a tree with N vertices may be labeled. Use the format shown in the examples below.
Example
Input: 2 3 4 5 0 Output: Case 1, N = 2, # of different labelings = 1 Case 2, N = 3, # of different labelings = 3 Case 3, N = 4, # of different labelings = 16 Case 4, N = 5, # of different labelings = 125
hide comments
|
|
klaus_9:
2019-07-09 09:10:59
got AC in one go....now i can finally read the question |
|
|
d_y1997:
2017-06-09 13:12:28
if for N = 9 and 10 , value obtained is in exponential then convert it in decimal ,,
|
|
|
cake_is_a_lie:
2017-04-04 09:42:08
It's obvious HOW to solve this, but if you want to understand WHY, you may want to read about Prüfer sequences. |
|
|
aakash_s:
2016-11-05 13:40:24
Stupid output format
|
|
|
marshal4world:
2016-10-31 14:01:54
take into consideration the typecasting of pow of variables ...
|
|
|
xunx:
2016-08-31 04:45:04
its easy to find pattern but can anyone explain the logic |
|
|
Gaurav Dahima:
2016-08-22 18:59:47
output format cost me 2 WA :( |
|
|
azam_9:
2016-07-04 12:08:25
no need to read the q jst observe the test cases and devive the formula..:D |
|
|
more_practice:
2016-06-27 20:25:16
nonisomorphic trees |
|
|
varma_msp:
2016-06-24 17:11:15
AC, without actually reading the question |
| Added by: | Camilo Andrés Varela León |
| Date: | 2007-10-07 |
| Time limit: | 0.100s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | North Central North America Regional Programming Contest - 2003 |

 RSS
RSS