MSE08H - GCD Determinant
| English | Vietnamese |
We say that a set S = {x1, x2, …, xn} is factor closed if for any xi ∈ S and any divisor d of xi we have d ∈ S. Let’s build a GCD matrix (S) = (sij), where sij = GCD(xi, xj) – the greatest common divisor of xi and xj. Given the factor closed set S, find the value of the determinant:
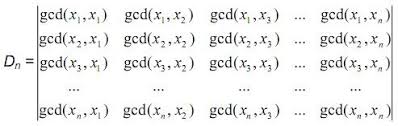
Input
The input file contains several test cases. Each test case starts with an integer n (0 < n < 1000), that stands for the cardinality of S. The next line contains the numbers of S: x1, x2, …, xn. It is known that each xi is an integer, 0 < xi < 2*10^9. The input data set is correct and ends with an end of file.
Output
For each test case find and print the value Dn mod 1000000007.
Sample
Input : 2 1 2 3 1 3 9 4 1 2 3 6 Ouput: 1 12 4
| Added by: | psetter |
| Date: | 2009-04-10 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | Southeastern European 2008 |

 RSS
RSS