PBOARD - Blocks for kids
Wango is a brilliant maths teacher. He has two sons Kango and Dango. They are born two years apart on the same day! Kango is 9 and Dango is 7. Their birthdays are approaching again. Wango has to buy them a gift each. After long thought, this time Wango wanted to give each of his sons a piece of the Pango board and thus introduce them to higher mathematics.
A size n (n >= 0) Pango board is a 2 by n rectangle of unit squares. A pango board has to be tiled with Pango pieces. Any tiling with the Pango pieces is acceptable. A size 0 Pango board exists and is unique and serves as an example of the empty set.
Four types of Pango pieces are available.
1 2 3 4
== == == ==
XX X X X
XX XX X
Picture of the four kinds of pieces
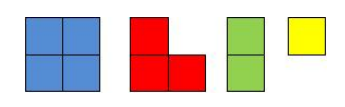
When Wango presents a board to Kango or Dango, he has to tile the board completely with these pieces (unlimited number of pieces of each type are available) and then give them out. Note that pieces cannot be rotated for tiling. To cut costs (recession mind you), Wango decides to buy a single board of size N, then choose a k (0 <= k <= N), and give a size k board to Kango and a size (N-k) board to Dango, (tiled of course). Help him find the number of ways he can give the presents. Two ways are distinct if and only if either Dango gets a different board or Kango gets a different board. Two Pango boards are considered the same if and only if they have the same tiling (same set of tiles at the same places) from left to right (rotation of board is not allowed in comparing).
Input
The input consists of a sequence of cases, one per line. Each case consists of one integer N (0 <= N <= 1000,000,000) representing the size of the board which Wango is going to buy. The input will end with a line containing -1. This case should not be processed. There will be a maximum of 10000 test cases.
Output
One line per case, outputting the number of ways Wango can distribute the presents to his sons modulo
10,007.
Example
Input:
0
1
2
-1
Output:
1
4
16
Explanation
Number of different 0-sized Pango boards = 1
Number of different 1-sized Pango boards = 2
Number of different 2-sized Pango boards = 6
For N = 0, he has to give 0-sized boards to both his sons. He can do this in 1*1 = 1 way
For N = 1, he has to give 0-sized board to one of his sons, and 1-sized board to the other, for a total of 2*1 +
1*2 = 4 ways
For N = 2, he can give the presents in 6*1 + 2*2 + 1*6 = 16 ways.
hide comments
|
|
nadstratosfer:
2020-01-04 03:03:31
The description is misleading; consider number of ways the kids can tile their respective boards themselves instead. Eg. tiling a n=2 with piece #1 and giving 1-sized piece to each kid is not a valid operation. |
|
|
Siddharth Kothari:
2010-09-02 18:07:24
The test cases don't contain n=0. My program failed for n=0, yet got an A.C. here.
|
|
|
Manukranth:
2010-09-02 18:07:24
There are a maximum of 10000 test cases.
|
|
|
Anna Piekarska:
2010-09-02 18:07:24
If I don't fail at input reading, there are a lot more cases than told in the statement. |
| Added by: | Manukranth |
| Date: | 2010-09-01 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: OBJC VB.NET |
| Resource: | ACM ICPC Amritapuri (India) Regionals 2008/2009 |

 RSS
RSS