POLY1 - Polygon
We say that two triangles intersect if their interiors have at least one common point. A polygon is called convex if every segment connecting any two of its points is contained in this polygon. A triangle whose vertices are also vertices of a convex polygon is called an elementary triangle of this polygon. A triangulation of a convex polygon is a set of elementary triangles of this polygon, such that no two triangles from the set intersect and a union of all triangles covers the polygon. We are given a polygon and its triangulation. What is the maximal number of triangles in this triangulation that can be intersected by an elementary triangle of this polygon?
Example
Consider the following triangulation:
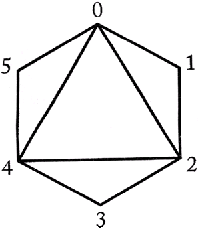
The elementary triangle (1,3,5) intersects all the triangles in this triangulation.
Task
Write a program that for each test case:
- reads the number of vertices of a polygon and its triangulation;
- computes the maximal number of triangles intersected by an elementary triangle of the given polygon;
- writes the result to standard output.
Input
The number of test cases t is in the first line of input, then t test cases follow separated by an empty line
In the first line of a test case there is a number n, 3 <= n <= 1000, which equals the number of vertices of the polygon. The vertices of the polygon are numbered from 0 to n-1 clockwise. The following n-2 lines describe the triangles in the triangulation. There are three integers separated by single spaces in the (i+1)-st line, where 1 <= i <= n-2. These are the numbers of the vertices of the i-th triangle in the triangulation.
Output
For each test case your program should produce one line with exactly one integer - the maximal number of triangles in the triangulation, that can be intersected by a single elementary triangle of the input polygon.
Example
Sample input: 1 6 0 1 2 2 4 3 0 5 4 2 4 0 Sample output: 4
| Added by: | Michał Czuczman |
| Date: | 2004-08-10 |
| Time limit: | 5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | 5th Polish Olympiad in Informatics, stage 1 (Krzysztof Diks) |

 RSS
RSS