POTHOLE - Potholers
A team of speleologists organizes a training in the Great Cave of Byte Mountains. During the training each speleologist explores a route from Top Chamber to Bottom Chamber. The speleologists may move down only, i.e. the level of every consecutive chamber on a route should be lower then the previous one. Moreover, each speleologist has to start from Top Chamber through a different corridor and each of them must enter Bottom Chamber using different corridor. The remaining corridors may be traversed by more than one speleologist. How many speleologists can train simultaneously?
Task
Write a program which:
- reads the cave description from the standard input,
- computes the maximal number of speleologists that may train simultaneously,
- writes the result to the standard output.
Input
The number of test cases t is in the first line of input, then t test cases follow separated by an empty line. In the first line of each test case there is one integer n (2<=n<=200), equal to the number of chambers in the cave. The chambers are numbered with integers from 1 to n in descending level order - the chamber of grater number is at the higher level than the chamber of the lower one. (Top Chamber has number 1, and Bottom Chamber has number n). In the following n-1lines (i.e. lines 2,3,...,n) the descriptions of corridors are given. The (i+1)-th line contains numbers of chambers connected by corridors with the i-th chamber. (only chambers with numbers grater then i are mentioned). The first number in a line, m, 0<=m<=(n-i+1), is a number of corridors exiting the chamber being described. Then the following m integers are the numbers of the chambers the corridors are leading to.
Output
Your program should write one integer for each test case. This number should be equal to the maximal number of speleologists able to train simultaneously,
Example
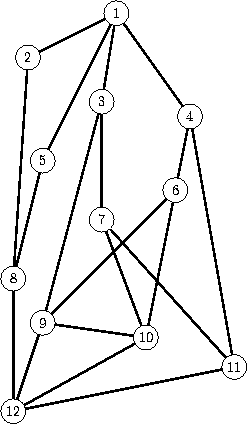
Sample input: 1 12 4 3 4 2 5 1 8 2 9 7 2 6 11 1 8 2 9 10 2 10 11 1 12 2 10 12 1 12 1 12 Sample output: 3
The sample input corresponds to the following cave:
hide comments
|
|
mostafamorsy2:
2021-07-27 16:53:22
Why i get TL I am using folk fulkerson algorithm like everyone |
|
|
leviathan1103:
2020-08-25 07:14:40
can anyone provide a tricky testcase.I don't know whats wrong with my code |
|
|
techmint:
2020-06-19 10:29:19
Finally found a problem to solve using edmonds karp improvision on ford fulkerson algorithm. |
|
|
akleberd:
2019-06-14 18:16:53
Be aware of double edges. |
|
|
lightyagami1:
2018-08-27 16:18:35
nice problem |
|
|
sharif ullah:
2018-07-06 21:59:22
every time clear graph array or graph vector!!!! |
|
|
nky_007:
2017-08-22 17:36:49
First on max-flow. |
|
|
cake_is_a_lie:
2017-04-04 12:47:12
Careful while reading the input: there are only N-1 adjacency lists, not N. |
|
|
vladimira:
2017-03-12 18:30:54
AC in one go! 1st question on flows. Learn some new python coding tricks. |
|
|
Anant Upadhyay:
2016-07-31 17:54:29
its a max flow problem do it using ford fulkerson algorithm |
| Added by: | Piotr Łowiec |
| Date: | 2004-09-13 |
| Time limit: | 7s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | 6th Polish Olympiad in Informatics, stage 2 |

 RSS
RSS