PROBLEM4 - PRIMITIVEROOTS
Introduction to Primitive Roots
a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n.
The number 3 is a primitive root modulo 7. because
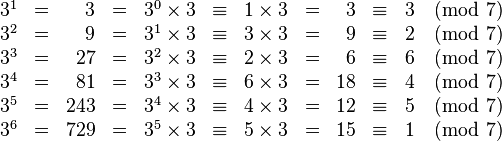
Problem Statement
Given a number n as input you’ve to find the (product all the primitive roots of n) % n if n is prime.
Input
The first line consists of T the number of test cases followed by T lines. Each line consists of a prime number n.
Output
For each test case print the test case number followed by ‘:’ followed by (product of all primitive roots of n) % n. If it is not a prime then print “NOTPRIME”
Input Specifications
1 <= T <= 100
3 <= n <= 10000
Example
Sample Input
3 6 7 9
Sample Output
1:NOTPRIME 2:1 3:NOTPRIME
Description for test case #2:
The primitive roots of 7 are 3 and 5. The product % 7 = 15%7 =1
hide comments
|
|
Piyush Kumar:
2015-06-16 08:54:40
Nice implementation of mathematics :) |
|
|
aqfaridi:
2014-03-13 19:18:35
@J.A.R.V.I.S. nice comment .. |
|
|
saket diwakar:
2014-03-13 19:18:35
don't deserve in classical....:P |
|
|
J.A.R.V.I.S.:
2014-03-13 19:18:35
PROBLEM4 kids :D |
|
|
Aradhya:
2014-03-13 19:18:35
for kids.. :D |
|
|
tainic:
2014-03-13 19:18:35
This is just a math problem, shouldn't be here. |
|
|
mukesh tiwari:
2014-03-13 19:18:35
Any particular reason for language restriction. Would it be possible to allow Haskell ? |
| Added by: | cegprakash |
| Date: | 2011-03-04 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | Edited question from Kurukshetra 2011 |

 RSS
RSS