PROG0014 - Collatz conjecture
The Collatz conjecture is a
conjecture from number theory. It is based on a sequence of numbers
— referred to as the hailstone sequence — that is
constructed in the following way: take any integer $n$. If $n$ is even,
divide it by 2 to get $n / 2$. If $n$ is odd, multiply it by 3 and add 1
to obtain $3n + 1$. The Collatz conjecture states that no matter what
integer $n$ ($n \geq 1$) you start with, you will eventually always reach
1. This conjecture has been first proposed by Lothar Collatz in 1937. Up
until now this conjecture has neither been proven nor rejected.
As an example, let's start from the number $n = 12$. The hailstone
sequence that results from this number reads as follows:
12, 6, 3, 10, 5, 16, 8, 4, 2, 1
Based on this sequence it is said that the cycle length for $n = 12$ is equal to 10, because the length of the corresponding hailstone sequence (including the last value 1) is equal to 10. If we start from the number $n = 15$, we have a much longer hailstone sequence with cycle length 18:
15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
For $n = 27$ the cycle length is as high as 112, climbing up to a maximal value above 9000 before descending to 1:
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
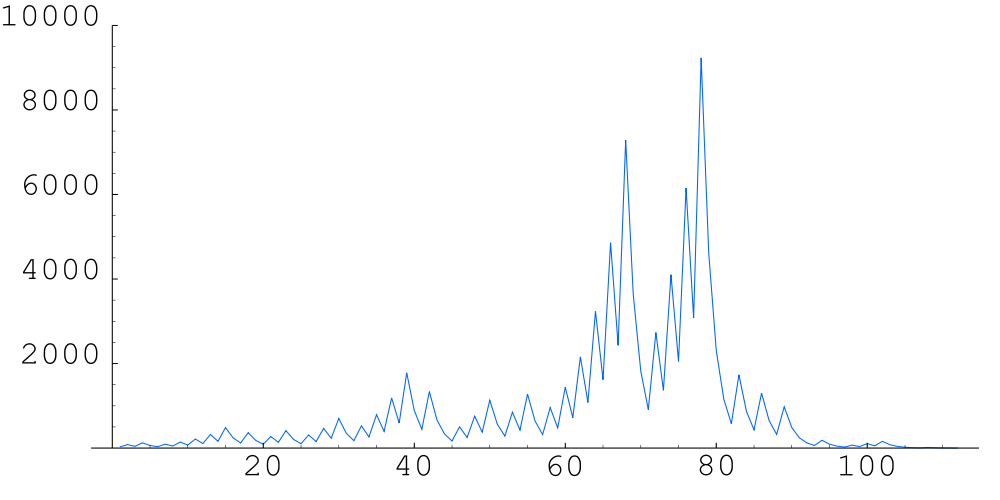
The figure below illustrates the evolution of the hailstone sequence for $n = 27$.
Input
The input contains $t$ test cases ($t \leq 100$). The first line of the input contains the integer $t$. It is followed by $t$ lines that each contain an integer $n$ ($n \geq 1$).
Output
For each test case, print the cycle length for $n$ on a separate line.
Example
Input:
5 1 2 321 1111111111111 111111111111111111111111111111111111111111111111111111111111
Output:
1 2 25 261 1296
Epilogue
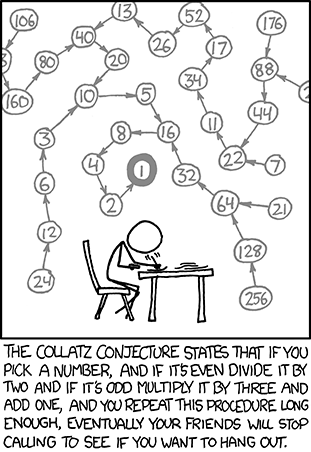
What's the use of the Collatz conjecture? The figure below shows a possible use case.
Het vermoeden van Collatz is
afkomstig uit de getaltheorie. Het is gebaseerd op een specifieke reeks
— een hagelsteen-reeks genoemd — die als volgt
geconstrueerd wordt: neem een willekeurig natuurlijk getal $n$. Als $n$
even is, dan wordt het gedeeld door 2. Als $n$ oneven is, dan wordt het
vermenigvuldigd met 3 en wordt daar nog 1 bij opgeteld. Het vermoeden van
Collatz zegt nu dat voor elk natuurlijk getal $n$ ($n \geq 1$) de
corresponderende hagelsteen-reeks altijd eindigt bij 1, als je het
beschreven proces maar lang genoeg herhaalt. Dit vermoeden werd voor het
eerst geformuleerd door Lothar Collatz in 1937. Tot op heden is het
vermoeden nog niet bevestigd of weerlegd.
Stel dat we bijvoorbeeld vertrekken van het getal $n = 12$, dan ziet de
corresponderende hagelsteen-reeks er als volgt uit:
12, 6, 3, 10, 5, 16, 8, 4, 2, 1
Men zegt dat de cyclelengte voor $n = 12$ gelijk is aan 10, omdat de lengte van de bijhorende hagelsteen-reeks (inclusief de laatste waarde 1) gelijk is aan 10. Als we echter vertrekken van het getal $n = 15$, dan ontstaat een veel langere reeks met cyclelengte 18:
15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
Voor $n = 27$ loopt de cyclelengte op tot 112, waarbij een maximale waarde bereikt wordt die al eens stuk boven de 9.000 ligt:
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
Onderstaande grafiek illustreert het verloop van de hagelsteen-reeks voor $n = 27$.
Invoer
De invoer bestaan uit $t$ testgevallen ($t \leq 100$). De eerste regel van de invoer bevat het natuurlijk getal $t$. Daarna volgen $t$ regels met op elke regel een natuurlijk getal $n$ ($n \geq 1$).
Uitvoer
Schrijf voor elk testgeval $n$ de corresponderende cyclelengte uit.
Voorbeeld
Invoer:
5 1 2 321 1111111111111 111111111111111111111111111111111111111111111111111111111111
Uitvoer:
1 2 25 261 1296
Epiloog
Waarvoor is het vermoeden van Collatz nuttig? Onderstaande figuur toont een mogelijke toepassing.
| Added by: | Peter Dawyndt |
| Date: | 2011-07-13 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS