PROG0122 - Number walks
There is one remarkable thing about randomness: its existence is neither proved nor disproved, notwithstanding the fact that it even appears everyday in science and in our everyday lives. For example, consider the constant number $\pi$: this number has an infinite number of decimal places with no recognizable pattern within the sequence. However, the distribution of the 10 possible digits is quite uniformly balanced — at least if we make a visual representation of, for example, the first million positions after the comma.
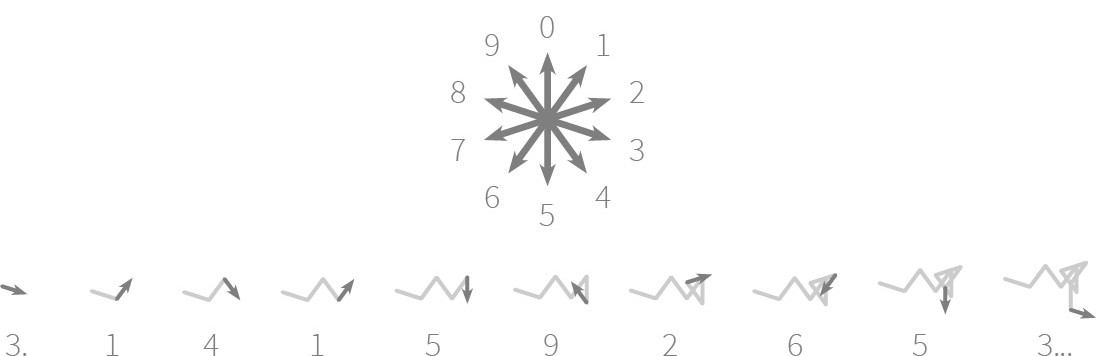
Generating such a visual representation is done in a fairly easy way. We always start in the origin $(0, 0)$. The we walk through the digits of the number from left to right. For each digit $c$ we turn clockwise in a direction that makes an angle of $c \times 36°$ relative to the positive Y-axis and take a step of length one forward. This is illustrated in the following figure for the first ten digits of the constant number $\pi$.
Representations of these kind of random walks are interesting for people who want to know more about the mystic character of this invisible companion. The first time they came to existence in 2009 in the masters thesis of Daniel A. Becker, and were refined later on in the Art in Pi project of Nadieh Bremer and the Number Walks project of Nicholas Rougeux. The work of this latter artist on a number of well known mathematical constants and irrational numbers like $\pi$, $e$ and the golden ratio have been bundled in the following sequence of video fragments.
Input
A single line that contains some text.
Output
A single line that contains the text Number g walks to position (x, y)., where g must be filled up with the given input text. The placeholders x and y must be filled up with the $(x, y)$-coordinates of the final position that is reached if we start in the origin, traverse all digits in the given input text from left to right, and for each digit take a step of length one in the direction described in the introduction. Both coordinates must be rounded up to two digits after the comma.
Example
Input:
3.141592653
Output:
Number 3.141592653 walks to position (3.44, -1.50).
Het bijzondere aan willekeurigheid is dat het bestaan ervan nog niet is bewezen — maar ook nog door niemand kon weerlegd worden — ondanks het feit dat we er elke dag mee geconfronteerd worden in de wetenschap en in ons dagelijkse leven. Neem bijvoorbeeld de constante $\pi$: dit getal heeft een oneindig aantal cijfers na de komma, zonder dat de reeks een herkenbaar patroon vertoont. Toch blijken de 10 mogelijke cijfers vrij uniform verdeeld te zijn over de reeks — tenminste als we een visuele voorstelling maken van bijvoorbeeld de eerste miljoen cijfers na de komma.
Het opbouwen van een dergelijke visuele voorstelling gebeurt vrij eenvoudig. We starten in de oorsprong $(0, 0)$. Daarna lopen we de cijfers van het getal af van links naar rechts. Voor elk cijfer $c$ draaien we ons in wijzerzin over een hoek van $c \times 36°$ ten opzichte van de positieve Y-as en zetten daarna een stap van lengte één vooruit. Dit wordt geïllustreerd in onderstaande figuur voor de eerste tien cijfers van het getal $\pi$.
Voorstellingen van dit soort dronkenmanswandelingen zijn interessant voor mensen die meer inzicht willen krijgen in de mystieke eigenschappen van willekeurigheid en de onzichtbare krachten die eraan ten grondslag liggen. Ze zagen voor het eerst het levenslicht in 2009 in de masterthesis van Daniel A. Becker, en werden later verfijnd in het Art in Pi project van Nadieh Bremer en het Number Walks project van Nicholas Rougeux. Het werk van deze laatste artiest met een aantal bekende wiskundige constanten en irrationale getallen zoals $\pi$, $e$ en de gouden snede werd gebundeld in onderstaande reeks videofragmenten.
Invoer
Eén regel tekst.
Uitvoer
De tekst Getal g wandelt naar positie (x, y)., waarbij g moet ingevuld worden met de tekst uit de invoer, en x en y moeten ingevuld worden met de $(x, y)$-coördinaten waar men eindigt, als men start in de oorsprong, alle cijfers van de gegeven tekst van links naar rechts afloopt, en voor elk cijfer een stap van lengte één zet in de richting die omschreven wordt in de inleiding. Hierbij moeten de coördinaten uitgeschreven worden met twee cijfers na de komma.
Voorbeeld
Invoer:
3.141592653
Uitvoer:
Getal 3.141592653 wandelt naar positie (3.44, -1.50).
| Added by: | Peter Dawyndt |
| Date: | 2011-08-06 |
| Time limit: | 10s-30s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


 RSS
RSS