PROG0224 - Zap reading
Reading a book from cover to cover, starting with the first page, turning, next page and so on until the last page - that's really outdated. Instead, we interpret the page number as a hyperlink: if we are done with page 14, we leap 14 pages ahead and start reading from there .
In a book with old page numbers we would jump from page 14 to page 28. If a hyperlink passes the last page, we go back to page one and start counting there. So if a book has 100 pages, and we just read page 74, then we count 26 pages until page 100, continue from page one and arrive at page 48 (for $26 + 48 = 74$). Note: that once you get to the last page (in this case, page 100), the fun is over, because by definition it hyperlinks to itself. Since the zap read program is fixed from beginning to end, the only degree of freedom is the number of pages $n$. The question that then presents itself is whether there are values of $n$ that make a book fully zap-readable? That is, no page remains unread.
Now we move away from the old page numbering. We can now divide the page numbers $1, 2, \ldots, n$ randomly over the $n$ pages. The number on a page - for example, page 17 - is still a hyperlink. After reading you will skip forward 17 pages. But there is no way of knowing the number of the page where you end up, because it can be any number from 1 to $n$ except 17. The question is, for which values of $n$ and a favorable order of the page numbers, are there books that are completely zap-readable? A taste: for a book with eight pages, two numberings are possible.It can be proven that with old-fashioned page numbering only the books with 1 and 2 pages are zap-readable. With books where the page numbering constitutes a permutation of the numbers $1, 2, \ldots, n$ all zap-readable books always have an even number of pages $n$ if $n > 1$. For an even number of pages $n$ a book can be made zap-readable providing the pages $1, 2, \ldots, n/2$ with a page numbering $n-1, n-3, n-5, \ldots, 1$ and providing the pages $n/2+1, n/2+2, \ldots, n$ with a page numbering $n, n-2, n-4, \ldots, 2$. If the number of pages $n$ is a power of two — in other words if $n = 2^m$ for $m \in \mathbb{N}$ — then a second construction method exists to make the book zap-readable. In this method page 1 gets the page number 1, and every next page that you read in zap read sequence gets one higher page number than the page that was read before.
Assignment
- Write a function zapreadable that returns a Boolean value for a given list of page numbers - that must be passed to the function as an argument - that indicates whether a book with this page numbering is zap-readable or not. Again, a book is zap-readable if the page numbers are a permutation of the integers $1, 2, \ldots, n$ and you get to read all the pages when zap reading (starting from the first page).
- Write a function zapbook that returns a list of page numbers that makes the book zap-readable. To this function, the number of pages $n$ ($n \in \mathbb{N}$ with $ n $> 0) of the book must be passed as argument. If $n$ is a power of two, then the list of page numbers must be built according to the second method of construction which was given above. For an even number of page numbers, or for $n = 1$ the first method of construction should be used. For an odd number of page numbers $ n> 1$ an empty list should be returned as a result, because in that case no zap-readable book can be constructed.
Example
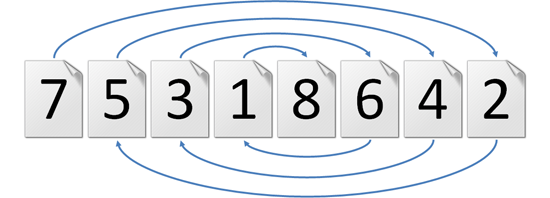
>>> zapreadable([7, 5, 3, 1, 8, 6, 4, 2]) True >>> zapreadable([1, 2, 4, 7, 3, 8, 6, 5]) False >>> zapreadable([1, 2, 5, 3, 8, 7, 4, 6]) True >>> zapreadable([1, 1, 1, 1, 1, 1, 1, 1]) False >>> zapbook(6) [5, 3, 1, 6, 4, 2] >>> zapbook(7) [] >>> zapbook(8) [1, 2, 5, 3, 8, 7, 4, 6]
Een boek van kaft tot kaft doorlezen, beginnend bij de eerste bladzijde, omslaan, volgende bladzijde en zo verder tot de laatste bladzijde — dat is werkelijk niet meer van deze tijd. In plaats daarvan vatten we het paginanummer op als hyperlink: als we pagina 14 uit hebben, bladeren we 14 pagina's verder en lezen daar door.
In een boek met ouderwetse paginanummering zouden we dus van pagina 14 naar pagina 28 springen. Als een hyperlink de laatste pagina voorbijschiet, gaan we terug naar pagina 1 en tellen daar door. Dus als een boek 100 pagina's heeft, en we hebben pagina 74 uit, dan tellen we 26 pagina's door tot pagina 100, gaan bij pagina 1 verder en komen uit bij pagina 48 (want $26 + 48 = 74$). Let wel: zodra je op de laatste pagina komt (in dit geval pagina 100) is het uit met de pret, want die hyperlinkt per definitie naar zichzelf. Aangezien het zapleestraject van begin tot eind vastligt, is de enige vrijheidsgraad het aantal pagina's $n$. De vraag die zich dan stelt is of er waarden van $n$ zijn die een boek volledig zapleesbaar maken? Dat wil zeggen: geen enkele pagina blijft ongelezen.
Vervolgens stappen we af van de ouderwetse paginanummering. We mogen nu de paginanummers $1, 2, \ldots, n$ willekeurig over de $n$ pagina's verdelen. Het nummer dat op een pagina staat — bijvoorbeeld pagina 17 — is dan nog steeds een hyperlink. Je bladert dus na lezing 17 pagina's door. Maar dat zegt niets over het nummer van de pagina waarop je dan terechtkomt, want dat kan elk getal van 1 tot en met $n$ behalve 17 zijn. De vraag is dan voor welke waarden van $n$ en een gunstig gekozen volgorde van de paginanummers er boeken zijn die volledig zapleesbaar zijn? Alvast een voorschotje: voor een boek met 8 pagina's zijn er twee nummeringen mogelijk.
Er kan aangetoond worden dat bij een ouderwetse paginanummering enkel de boeken met 1 en 2 pagina's zapleesbaar zijn. Bij boeken waarbij de paginanummering een permutatie vormt van de nummers $1, 2, \ldots, n$ hebben alle zapleesbare boeken steeds een even aantal pagina's $n$ als $n > 1$. Voor een even aantal pagina's $n$ kan men een boek zapleesbaar maken door de pagina's $1, 2, \ldots, n/2$ een paginanummering $n-1, n-3, n-5, \ldots, 1$ te geven en door de pagina's $n/2+1, n/2+2, \ldots, n$ een paginanummering $n, n-2, n-4, \ldots, 2$ te geven. Indien het aantal pagina's $n$ een macht van twee is — met andere woorden als $n = 2^m$ voor $m \in \mathbb{N}$ — dan bestaat er een tweede constructiemethode om het boek zapleesbaar te maken. Bij deze methode krijgt pagina 1 het paginanummer 1, en krijgt elke volgende pagina die je leest in zapleesvolgorde steeds één paginanummer hoger dan deze van de pagina die daarvoor werd gelezen.
Opgave
- Schrijf een functie zapleesbaar die voor een gegeven lijst van paginanummers — die als argument aan de functie moet doorgegeven worden — een Booleaanse waarde teruggeeft die aangeeft of een boek met deze paginanummering zapleesbaar is of niet. Nogmaals, een boek is zapleesbaar als de paginanummers een permutatie vormen van de getallen $1, 2, \ldots, n$ en je bij het zaplezen (vertrekkend vanaf de eerste pagina) alle pagina's te lezen krijgt.
- Schrijf een functie zapboek die een lijst van paginanummers teruggeeft die het boek zapleesbaar maakt. Aan deze functie moet het aantal pagina's $n$ ($n \in \mathbb{N}$ met $n > 0$) van het boek als argument doorgegeven worden. Indien $n$ een macht van twee is, dan moet de lijst van paginanummers opgebouwd worden volgens de tweede constructiemethode die hierboven gegeven werd. Voor een even aantal paginanummers of voor $n=1$ moet de eerste constructiemethode gebruikt worden. Voor een oneven aantal paginanummers $n > 1$ moet een lege lijst als resultaat teruggegeven worden, omdat in dat geval geen zapleesbaar boek kan geconstrueerd worden.
Voorbeeld
>>> zapleesbaar([7, 5, 3, 1, 8, 6, 4, 2]) True >>> zapleesbaar([1, 2, 4, 7, 3, 8, 6, 5]) False >>> zapleesbaar([1, 2, 5, 3, 8, 7, 4, 6]) True >>> zapleesbaar([1, 1, 1, 1, 1, 1, 1, 1]) False >>> zapboek(6) [5, 3, 1, 6, 4, 2] >>> zapboek(7) [] >>> zapboek(8) [1, 2, 5, 3, 8, 7, 4, 6]
| Added by: | Peter Dawyndt |
| Date: | 2012-02-12 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


 RSS
RSS