PROG0266 - Marsaglia method
Preparation
The module random from the Standard Python Library can be used for (amongst other things) generating random numbers. The function random() from this module generates a random real number from the interval $[0, 1[$. The function randint(a, b) on the other hand, can be used to generate a random integer from the interval $[a, b]$. The interactive Python session below indicates how you can use the functions from the random module with some examples.
>>> import random >>> help(random.random) Help on built-in function random: random(...) random() -> x in the interval [0, 1). >>> random.random() 0.954131645221452 >>> random.random() 0.3548429482674793 >>> help(random.randint) Help on method randint in module random: randint(self, a, b) method of random.Random instance Return random integer in range [a, b], including both end points. >>> random.randint(3, 10) 5 >>> random.randint(3, 10) 8
Description
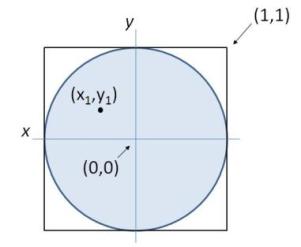
A sphere can be represented as a collection of all points on a distance $r$ from the central point $(0,0,0)$. If $r=1$, it is named a unit sphere. The Marsaglia method can be used to generate a random point on a sphere with radius $r$. In a first step of this method, a random point $(x_1,y_1)$ is chosen that lays within the unit sphere. To this point applies that: $x_1^2+y_1^2\leq 1$. In order to do this, random points are generated in the 2-by-2 square $[-1,1]\times[-1,1]$ with centre in $(0,0)$, until a point is found that lays within the unit sphere.
The point $(x_1,y_1)$ is used in the following way to determine the $(x,y,z)$ co-ordinates of a random point on a circle with radius $r$: \[ \begin{aligned} x & = 2 r x_1 \sqrt{1 - x_1^2 - y_1^2} \\ y & = 2 r y_1 \sqrt{1 - x_1^2 - y_1^2} \\ z & = r - 2r(x_1^2 + y_1^2) \end{aligned} \]
Assignment
Write a function that can be used to generate a random point on a sphere with radius $r \in \mathbb{R}$. A value for $r$ can be given to the function optionally. Standard, the random point is generated on the unit sphere. The function must print a tuple with the $(x,y,z)$ co-ordinates of the random point.
Example
>>> spherecoordinate() (0.8208783192500947, 0.24904502507471912, 0.5139410087458212) >>> spherecoordinate() (0.1705946803883025, 0.9853183076681309, 0.006729606022916168) >>> spherecoordinate() (0.5245775493577824, 0.47160784998323607, -0.7088049312356488) >>> spherecoordinate(1.2) (1.006669684101887, 0.41835600224171376, 0.10767730725894864) >>> spherecoordinate(5.8) (0.3653448756504214, 0.8635619785170504, -2.2182839834195476) >>> spherecoordinate(4.9) (0.5245775493577824, 0.47160784998323607, -0.7088049312356488)
Voorbereiding
De module random uit de Standard Python Library kan onder andere gebruikt worden om willekeurige getallen te genereren. De functie random() uit deze module genereert een willekeurig reëel getal uit het interval $[0, 1[$. De functie randint(a, b) kan dan weer gebruikt worden om een willekeurig geheel getal te genereren uit het interval $[a, b]$. Onderstaande interactieve Python sessie geeft aan de hand van enkele voorbeelden aan hoe je de functies uit de module random kunt gebruiken.
>>> import random >>> help(random.random) Help on built-in function random: random(...) random() -> x in the interval [0, 1). >>> random.random() 0.954131645221452 >>> random.random() 0.3548429482674793 >>> help(random.randint) Help on method randint in module random: randint(self, a, b) method of random.Random instance Return random integer in range [a, b], including both end points. >>> random.randint(3, 10) 5 >>> random.randint(3, 10) 8
Omschrijving
Een bol kan voorgesteld worden als de verzameling van alle punten op afstand $r$ vanaf het centraal punt $(0,0,0)$. Indien $r=1$ dan spreekt men van de eenheidsbol. De methode van Marsaglia kan gebruikt worden om een willekeurig punt op een bol met straal $r$ te genereren. In een eerste stap van deze methode wordt een willekeurig punt $(x_1,y_1)$ gekozen dat binnen de eenheidscirkel gelegen is. Dit is een punt waarvoor geldt dat $x_1^2+y_1^2\leq 1$. Om dit te doen worden willekeurige punten gegenereerd in het 2-bij-2 vierkant $[-1,1]\times[-1,1]$ met centrum in $(0,0)$, totdat een punt gevonden wordt dat binnen de eenheidscirkel ligt.
Het punt $(x_1,y_1)$ wordt vervolgens gebruikt om op de volgende manier de $(x,y,z)$ coördinaten van een willekeurig punt op de bol met straal $r$ te bepalen: \[ \begin{aligned} x & = 2 r x_1 \sqrt{1 - x_1^2 - y_1^2} \\ y & = 2 r y_1 \sqrt{1 - x_1^2 - y_1^2} \\ z & = r - 2r(x_1^2 + y_1^2) \end{aligned} \]
Opgave
Schrijf een functie waarmee een willekeurig punt op een bol met straal $r \in \mathbb{R}$ kan gegeneerd worden. Aan deze functie kan optioneel een waarde voor $r$ doorgegeven worden. Standaard wordt een willekeurig punt op de eenheidsbol gegenereerd. De functie moet als resultaat een tuple met de $(x,y,z)$ coördinaten van het willekeurige punt teruggeven.
Voorbeeld
>>> bolcoordinaat() (0.8208783192500947, 0.24904502507471912, 0.5139410087458212) >>> bolcoordinaat() (0.1705946803883025, 0.9853183076681309, 0.006729606022916168) >>> bolcoordinaat() (0.5245775493577824, 0.47160784998323607, -0.7088049312356488) >>> bolcoordinaat(1.2) (1.006669684101887, 0.41835600224171376, 0.10767730725894864) >>> bolcoordinaat(5.8) (0.3653448756504214, 0.8635619785170504, -2.2182839834195476) >>> bolcoordinaat(4.9) (0.5245775493577824, 0.47160784998323607, -0.7088049312356488)
| Added by: | Peter Dawyndt |
| Date: | 2012-08-27 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS