PROG0273 - Washing machine
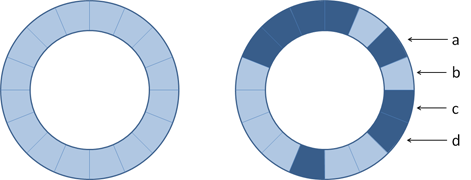
Suppose that we have subdivided the rotating drum of a washing machine into sixteen equal parts, as shown in the left figure below. The dark segments represent conductive materials, whereas the lighter segments represent non-conductive materials. The position of the drum is represented by four binary digits $a$, $b$, $c$ and $d$ as shown in the right figure below. Depending on the position of the drum, the connection points represented by $a$, $b$, $c$ en $d$ either are grounded or insulated from the earth — in the example figure below the grounded connection points are $a$, $c$ and $d$. Grounded connection points send out a signal that is represented by 1, and isolated connection points send out a signal represented by 0.
In order to ensure that each of the sixteen positions of the rotating drum can be represented in a unique way by a word $abcd$ of four binary digits, the conductive and non-conductive materials need to be allocated to the sixteen segments in such a way that each of the sixteen possible words of four binary digits $abcd$ occurs. The question that arises is whether this is possible. And if so, then how can the materials be ranked?
The right figure above immediately gives a solution to this problem. The position shown corresponds to the binary word 1011. If we rotate the drum counterclockwise we successively obtain the following sequence of binary words:
0110, 1100, 1001, 0010, 0100, 1000, 0000, 0001,
0011, 0111, 1111, 1110, 1101, 1010, 0101, 1011.
All of these words of four binary words are different, and together they form the sixteen possible positions of the rotating drum.
The problem of the rotating drum and its solution based on de Bruijn sequences, finds applications in computational biology, the generation of pseudo-random numbers, cryptography, telecommunications, and yes, even in the design of washing machines.
Algorithm
A de Bruijn sequence of order $n$ is a shortest possible (circular) binary string such that every sequence of $n$ bits appears as a substring at least once. For example, the string 0000111101100101 is a de Bruijn sequence of order 4, and all $2^4$ possible 4-bit sequences (0000, 0001, …, 1111) occur exactly once. A possible algorithm to generate a de Bruijn sequence of order $n$ works as follows:
- start with a string of $n$ consecutive zeroes
- append 1 to the end of the string if the $n$-digit suffix that would be formed this way has not already appeared in the sequence; otherwise a 0 is appended to the end of the string
- repeat step 2 until the length of the sequence equals $2^n$
Input
An integer $n \in \mathbb{N}_0$.
Output
The de Bruijn sequence of order $n$ that results from the algorithm given above.
Example
Input:
4
Output:
0000111101100101
Stel dat we het oppervlak van de roterende trommel van een wasmachine in zestien gelijke delen verdelen, zoals aangegeven in de linker figuur hieronder. De donkere delen stellen geleidende materialen voor, en de lichte delen niet-geleidende materialen. We stellen de positie van de trommel voor aan de hand van vier binaire cijfers $a$, $b$, $c$ en $d$ zoals aangegeven in de rechter figuur hieronder. Afhankelijk van de positie van de trommel zijn de uiteinden die worden voorgesteld door $a$, $b$, $c$ en $d$ ofwel geaard of geïsoleerd van de aarde — in onderstaande figuur zijn de geaarde uiteinden bijvoorbeeld $a$, $c$ en $d$. De geaarde eindpunten sturen een signaal uit dat wordt voorgesteld door 1, en de geïsoleerde einpunten stellen een signaal uit dat wordt voorgesteld door 0.
Om ervoor te zorgen dat elk van de zestien posities van de trommels op een unieke manier kan voorgesteld worden door een woord $abcd$ van vier binaire cijfers, moeten de geleidende en niet-geleidende materialen op zo'n manier aan de zestien delen toegekend worden dat elk van de zestien mogelijke woorden van vier binaire cijfers $abcd$ voorkomen. De vraag die zich stelt is of dit wel mogelijk is. En indien ja, hoe kunnen de materialen dan gerangschikt worden?
De rechter figuur hierboven geeft meteen ook een oplossing voor dit probleem. De positie die getoond wordt correspondeert met het binaire woord 1011. Als we de trommel in tegenwijzerzin roteren dan krijgen we achtereenvolgens de volgende binaire woorden:
0110, 1100, 1001, 0010, 0100, 1000, 0000, 0001,
0011, 0111, 1111, 1110, 1101, 1010, 0101, 1011.
Deze woorden van vier binaire cijfers zijn allemaal verschillend, en stellen elk van de zestien mogelijke posities van de roterende trommel voor.
Het probleem van de roterende trommel en de oplossing op basis van de Bruijn reeksen, vindt toepassingen in de computationele biologie, de productie van pseudo-willekeurige getallen, de cryptografie, de telecommunicatie, en ja, zelfs bij het ontwerpen van wasmachines.
Algoritme
Een de Bruijn reeks van orde $n$ is de kortst mogelijke (circulaire) binaire string waarin elk mogelijk woord van $n$ bits tenminste één keer voorkomt als deelstring. Zo is de string 0000111101100101 bijvoorbeeld een de Bruijn reeks van orde 4, waarbij elk van de $2^4$ mogelijke binaire woorden van lengte 4 (0000, 0001, …, 1111) juist één keer voorkomen. Een mogelijk algoritme om een de Bruijn reeks van orde $n$ op te stellen werkt als volgt:
- start met een string van $n$ opeenvolgende nullen
- voeg achteraan een 1 toe als het $n$-tuple dat daarmee gevormd wordt nog niet in de string voorkomt; anders voeg je achteraan een 0 toe
- herhaal stap 2 totdat de lengte van de string gelijk is aan $2^n$
Invoer
Een natuurlijk getal $n \in \mathbb{N}_0$.
Uitvoer
De de Bruijn reeks van orde $n$ die je bekomt op basis van bovenstaand algoritme.
Voorbeeld
Invoer:
4
Uitvoer:
0000111101100101
| Added by: | Peter Dawyndt |
| Date: | 2012-08-27 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS