PROG0362 - Bread crumbs
Twins Hansel and Gretel live deep in a forest with their father and stepmother. To prevent that his children would get lost while they are playing in the forest, father has drawn a square grid on a map of the forest where two consecutive grid lines always are separated 50 meters from each other. Their house is positioned on the map at the location with co-ordinates $(0, 0)$. Father has marked the trees in the forest that are located at a crossing of two grid lines using a yellow ribbon that contains the $(x, y)$ coordinates of the tree, with the $x$-coordinate indicating the number of vertical grid lines the tree is positioned to the right of the house, and the $y$-coordinate indicating the number of horizontal grid lines the tree is positioned to the above the house.
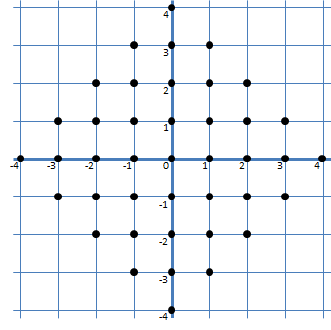
When the children leave their house to play in the forest, father only allows them to move to the next tree with a yellow ribbon that is to the right, to the left, above or below their current position if the sum of the digits of the $x$-coordinate and the $y$-coordinate on the ribbon is not higher than their age (expressed in years). The tree at position $(12, 24)$ can thus only be reached if they are at least $1 + 2 + 2 + 4 = 9$ years old. At each tree they visit they should also leave a breadcrumb in order not to loose their way back home. Hansel and Gretel now have a tradition at each birthday to calculate the number of points in the forest (their house and trees marked by a yellow ribbon) they will be able to reach during the next year. At the age of four, they have marked the following 41 reachable points on a map of the forest.
Note that when Hansel and Gretel are 10 years or older, it will no longer be the case that all reachable points around their house form a a square (rotated by 45 degrees). We show some additional figures below, that display the reachable points in white when Hansel and Gretel are $n$ years old.
Assignment
- Write a function reachable that takes two arguments. The first argument is a tuple $(x,y)$ that represents the coordinates of a point in the forest ($x, y \in \mathbb{Z}$). The second argument is a number $n \in \mathbb{N}$. The function must return a Boolean value indicating whether or not the sum of the digits of the $x$- and $y$-coordinate is lower than or equal to $n$.
- Write a function neighbours that takes a tuple $(x,y)$ representing the coordinates of a point in the forest ($x, y \in \mathbb{Z}$). The function must return a set of $(x,y)$-coordinates containing the four points that are 50 meters away from the given point.
- Use the functions reachable and neighbours to write a function breadcrumbs that takes an integer $n \in \mathbb{N}$. This integer represents the age (in years) of Hansel and Gretel. The function must return the set of all points in the forest that Hans and Gretel can reach at the given age.
Algorithm
- initialisation: $\mathcal{B} = \emptyset,\mathcal{R} = \{(0, 0)\}$
- remove a random point $p$ from $\mathcal{R}$
- add $p$ to $\mathcal{B}$
- add all neighbors of $p$ to $\mathcal{R}$ that are reachable and are not already in $\mathcal{B}$
- repeat from step 2 until $\mathcal{R} = \emptyset$
Here, $\emptyset$ represents the empty set.
Example
>>> reachable((0, 0), 0) True >>> reachable((10, 20), 3) True >>> reachable((2, 3), 4) False >>> neighbours((0, 0)) {(0, 1), (0, -1), (1, 0), (-1, 0)} >>> neighbours((4, 3)) {(4, 2), (4, 4), (3, 3), (5, 3)} >>> breadcrumbs(0) {(0, 0)} >>> breadcrumbs(2) {(0, 1), (-1, 1), (0, 0), (-1, 0), (0, -2), (0, 2), (2, 0), (-1, -1), (0, -1), (1, 0), (1, -1), (1, 1), (-2, 0)} >>> len(breadcrumbs(10)) 1121 >>> len(breadcrumbs(19)) 102485
De tweeling Hans en Grietje woont met vader en stiefmoeder temidden van een uitgestrekt bos. Om te voorkomen dat zijn kinderen tijdens hun spel zouden verdwalen, heeft vader op een kaart van het bos een rechthoekig rooster getekend waarbij opeenvolgende roosterlijnen telkens op 50 meter afstand van elkaar liggen. Hun huis is op die kaart gelegen op het punt met coördinaat $(0, 0)$. Aan de bomen in het bos die op de kruising van twee roosterlijnen liggen, heeft vader een geel lintje bevestigd met daarop de $(x, y)$ coördinaten van de boom, waarbij de $x$-coördinaat aangeeft op hoeveel verticale roosterlijnen rechts van het huis de boom staat en de $y$-coördinaat aangeeft horizontale roosterlijnen boven het huis de boom staat.
Als de kinderen hun huis verlaten om het bos in te trekken, dan mogen ze van vader telkens naar een volgende boom met een geel lintje gaan die zich op 50 meter boven, onder, links of rechts van hun huidige positie bevindt als de som van de cijfers van de $x$-coördinaat en de $y$-coördinaat op het lintje aan die boom niet groter is dan hun leeftijd (uitgedrukt in jaren). De boom op positie $(12, 24)$ kunnen ze dus enkel bereiken als ze ten minste $1 + 2 + 2 + 4 = 9$ jaar oud zijn. Bij elke boom die ze bezoeken moeten ze ook een broodkruimel achterlaten om hun weg niet te verliezen. Hans en Grietje maken er bij elke verjaardag dan ook een spelletje van om te berekenen hoeveel punten in het bos (hun huis en de bomen waaraan een geel lintje hangt) ze dat jaar zullen kunnen bereiken. Op onderstaande kaart hebben ze de 41 punten aangeduid die ze vanaf hun vierde verjaardag kunnen bereiken.
Merk op dat als Hans en Grietje tien jaar of ouder zijn, het niet langer zo is dat alle punten binnen een vierkant (45 graden geroteerd) rondom hun huis bereikbaar zijn. Hieronder tonen we nog een aantal figuren waarop de bereikbare punten in het wit staan aangegeven als Hans en Grietje $n$ jaar oud zijn.
Opgave
- Schrijf een functie bereikbaar waaraan twee argumenten moeten doorgegeven worden. Het eerste argument is een tuple $(x,y)$ dat de coördinaat van een punt in het bos voorstelt ($x, y \in \mathbb{Z}$). Het tweede argument is een getal $n \in \mathbb{N}$. De functie moet een Booleaanse waarde teruggeven die aangeeft of de som van de cijfers van de $x$- en $y$-coördinaat kleiner of gelijk is aan $n$.
- Schrijf een functie buren waaraan een tuple $(x,y)$ moet doorgegeven worden dat de coördinaat van een punt in het bos voorstelt ($x, y \in \mathbb{Z}$). De functie moet een verzameling teruggeven met de $(x,y)$-coördinaten van de vier punten die op 50 meter afstand van het gegeven punt liggen.
- Gebruik de funties bereikbaar en buren om een functie broodkruimels te schrijven waaraan een getal $n \in \mathbb{N}$ moet doorgegeven worden. Dat getal stelt de leeftijd (in jaren) van Hans en Grietje voor. De functie moet een verzameling van alle punten in het bos teruggeven die Hans en Grietje dat jaar kunnen bereiken.
Algoritme
- initialisatie: $\mathcal{B} = \emptyset,\mathcal{R} = \{(0, 0)\}$
- haal een willekeurig punt $p$ uit $\mathcal{R}$
- voeg $p$ toe aan $\mathcal{B}$
- voeg de buren van $p$ toe aan $\mathcal{R}$ als die buren bereikbaar zijn en nog niet in $\mathcal{B}$ zitten
- herhaal vanaf stap 2 totdat $\mathcal{R} = \emptyset$
Hierbij stelt $\emptyset$ de lege verzameling voor.
Voorbeeld
>>> bereikbaar((0, 0), 0) True >>> bereikbaar((10, 20), 3) True >>> bereikbaar((2, 3), 4) False >>> buren((0, 0)) {(0, 1), (0, -1), (1, 0), (-1, 0)} >>> buren((4, 3)) {(4, 2), (4, 4), (3, 3), (5, 3)} >>> broodkruimels(0) {(0, 0)} >>> broodkruimels(2) {(0, 1), (-1, 1), (0, 0), (-1, 0), (0, -2), (0, 2), (2, 0), (-1, -1), (0, -1), (1, 0), (1, -1), (1, 1), (-2, 0)} >>> len(broodkruimels(10)) 1121 >>> len(broodkruimels(19)) 102485
| Added by: | Peter Dawyndt |
| Date: | 2013-04-03 |
| Time limit: | 20s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


 RSS
RSS