PROG0442 - Nonogram
A Nonogram is a Japanese picture puzzle in which a hidden picture can be found. This image can be formed by colouring the boxes of a rectangular lattice black or white, taking into account the set of integers that is specified for each row and each column of the grid. These numbers indicate how many consecutive black squares there should be in that row or column. For example, if the grid indicates the series 4 8 3 , this means that the row or column is made up of sets of four, eight, and three consecutive black boxes, in that order, and that there is at least one white box between each of the consecutive series.
Assignment
For this task, you must solve a simplified version of the Nonogram puzzle. As with the original puzzle, the sequences of black boxes in each row are provided. The description for the columns, however, is no longer needed. For each set of consecutive black boxes is now defined by a couple of integers $(s, l)$, where $s$ and $l$ indicate the start position and the length of the series, respectively. The far-left cell of a row is at position zero.
Note that the order in which the sequences of consecutive black boxes are given no longer plays a role. A row of a Nonogram puzzle can thus be defined by a series of number pairs that indicate the start position and the length of the series, respectively, of the consecutive black boxes.
Input
The input defines the specifications of a simplified Nonogram puzzle. The first line of the input contains two integers $h$ and $b$ which indicate the height and the width of the image. The two numbers are separated from each other by a single space. This is followed by $h$ lines that each describe another line of the hidden image. This description consists of pairs of integers: each pair consists of two integers, separated by a comma and enclosed in parentheses. The pairs themselves are each separated by a comma. Except between the figures of the same integer, spaces can be everywhere. The first and second number of each pair indicate the starting position and length, respectively, of a succession of black boxes on the line of the image.
Output
Example
Input:
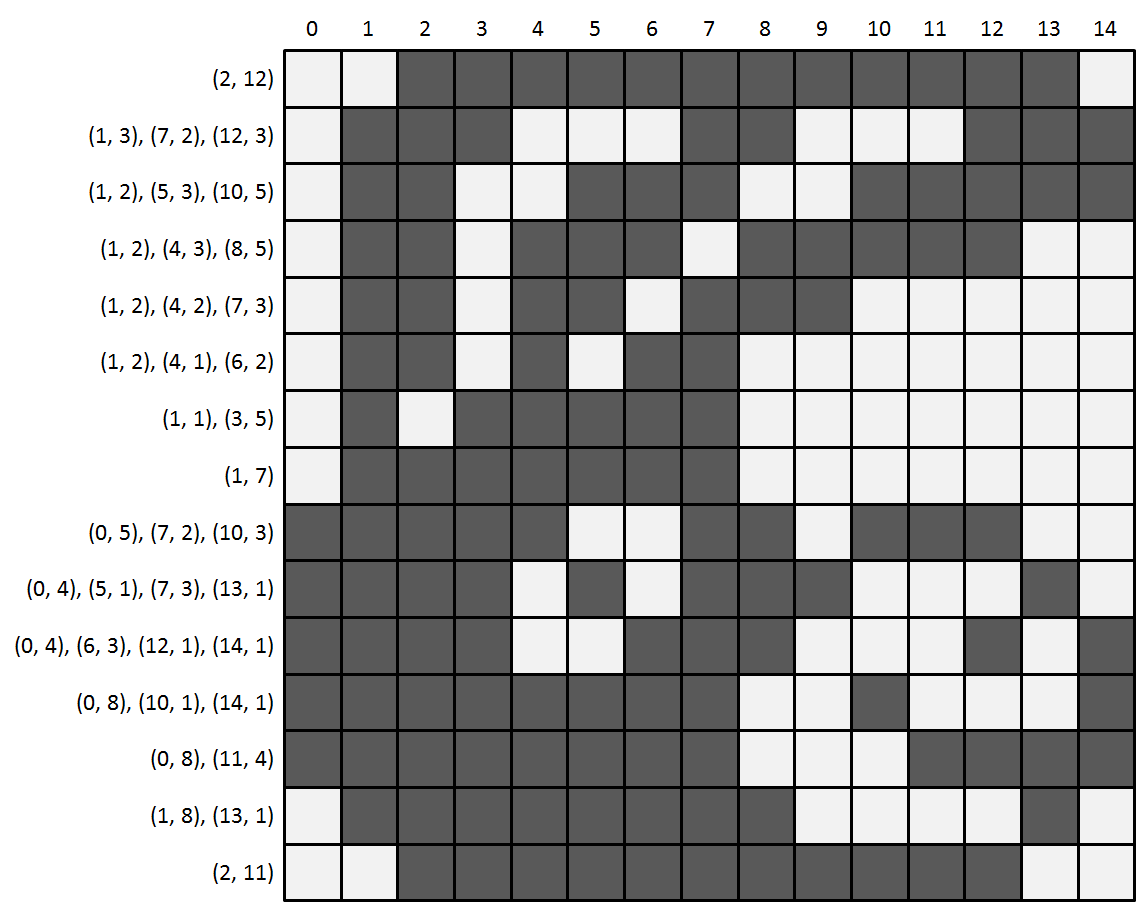
15 15
(2, 12)
(1, 3), (7, 2), (12, 3)
(1, 2), (5, 3), (10, 5)
(1, 2), (4, 3), (8, 5)
(1, 2), (4, 2), (7, 3)
(1, 2), (4, 1), (6, 2)
(1, 1), (3, 5)
(1, 7)
(0, 5), (7, 2), (10, 3)
(0, 4), (5, 1), (7, 3), (13, 1)
(0, 4), (6, 3), (12, 1), (14, 1)
(0, 8), (10, 1), (14, 1)
(0, 8), (11, 4)
(1, 8), (13, 1)
(2, 11)
Output:
############
### ## ###
## ### #####
## ### #####
## ## ###
## # ##
# #####
#######
##### ## ###
#### # ### #
#### ### # #
######## # #
######## ####
######## #
###########
Een nonogram is een Japanse beeldpuzzel waarbij een verborgen afbeelding moet gevonden worden. Deze afbeelding kan gevormd worden door de vakjes van een rechthoekig rooster zwart of wit te kleuren, rekening houdend met de reeks natuurlijke getallen die voor elke rij en elke kolom van het rooster wordt opgegeven. Deze getallen geven aan hoeveel opeenvolgende zwarte vakjes er op die rij of kolom staan. Als de opgave bijvoorbeeld de getallenreeks 4 8 3 aangeeft, betekent dit dat de rij of kolom bestaat uit reeksen van vier, acht en drie opeenvolgende zwarte vakjes, in die volgorde, en dat er minstens één wit vakje staat tussen elk van deze opeenvolgende reeksen.
Opgave
Voor deze opgave moet je een vereenvoudigde versie van de nonogrampuzzel oplossen. Zoals bij de originele puzzel worden voor elke rij de reeksen opeenvolgende zwarte vakjes opgegeven. De omschrijving voor de kolommen hebben we echter niet langer nodig. Elke reeks opeenvolgende zwarte vakjes wordt nu immers omschreven door een koppel natuurlijke getallen $(s, l)$, waarbij $s$ en $l$ respectievelijk de startpositie en de lengte van de reeks aangeven. Het meest linkse vakje van een rij staat hierbij op positie nul.
Merk op dat de volgorde waarin de reeksen
opeenvolgende zwarte vakjes worden opgegeven nu niet langer een rol
speelt. Een rij van een nonogrampuzzel kan dus omschreven worden door een
reeks getallenparen die respectievelijk de startpositie en de lengte van
de reeks opeenvolgende zwarte vakjes aangeven.
Invoer
De invoer omschrijft de opgave van een vereenvoudigde nonogrampuzzel. De eerste regel van de invoer bevat twee natuurlijke getallen $h$ en $b$ die respectievelijk de hoogte en de breedte van de afbeelding aangeven. De twee getallen worden van elkaar gescheiden door één enkele spatie. Daarna volgen $h$ regels die telkens een volgende regel van de verborgen afbeelding omschrijven. Deze omschrijving bestaat uit koppels natuurlijke getallen: elk koppel bestaat uit twee natuurlijke getallen, van elkaar gescheiden door een komma en ingesloten tussen ronde haakjes. De koppels zelf worden telkens van elkaar gescheiden door een komma. Behalve tussen de cijfers van eenzelfde natuurlijk getal, mogen binnen de omschrijving voorts op elke plaats spaties staan. Het eerste en tweede getal van elk koppel geven respectievelijk de startpositie en de lengte aan van een reeks opeenvolgende zwarte vakjes op de regel van de afbeelding.
Uitvoer
Voorbeeld
Invoer:
15 15
(2, 12)
(1, 3), (7, 2), (12, 3)
(1, 2), (5, 3), (10, 5)
(1, 2), (4, 3), (8, 5)
(1, 2), (4, 2), (7, 3)
(1, 2), (4, 1), (6, 2)
(1, 1), (3, 5)
(1, 7)
(0, 5), (7, 2), (10, 3)
(0, 4), (5, 1), (7, 3), (13, 1)
(0, 4), (6, 3), (12, 1), (14, 1)
(0, 8), (10, 1), (14, 1)
(0, 8), (11, 4)
(1, 8), (13, 1)
(2, 11)
Uitvoer:
############
### ## ###
## ### #####
## ### #####
## ## ###
## # ##
# #####
#######
##### ## ###
#### # ### #
#### ### # #
######## # #
######## ####
######## #
###########
| Added by: | Peter Dawyndt |
| Date: | 2014-01-20 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS