PROG0570 - Triton City
For thousands of years cities have been the manifestation of humankind's artistry, imagination, and instinct to succeed. They embody our strong social desires and longing to create grand masterpieces. London, Constantinople, Paris, New York, Ancient Rome and Tokyo have been just a few of the dazzling trophies mankind has built. But there have been many cases in which someone's vision for a better, more efficient, or more fantastic city collapsed into a heap of broken dreams.
Buckminster Fuller was a brilliant visionary, architect, scientist, environmentalist and philosopher who, in the 1960s, developed a bold design for a floating utopia that was dubbed Triton City (below). It would have been assembled from tetrahedral modules, starting with a floating neighborhood of 5000 residents, with an elementary school, a supermarket and a few specialty shops. Three to six neighborhoods would form a town, and three to seven towns would form a city. At each stage the corresponding infrastructure would be added: schools, civic facilities, government offices, and industry. A full-sized city might accommodate 100.000 people in a single building.
Fuller was initially commissioned by a wealthy Japanese patron to design a floating city for Tokyo Bay. He died in 1966, but astoundingly enough, the United States Department of Urban Development (HUD) commissioned Fuller for further design and analysis. His designs called for the city to be resistant to tsunamis, provide the most possible outside living, desalinate the very water that it would float in for consumption, give privacy to each residence, and incorporate a tetrahedronal shape which provides the most surface area with the least amount of volume. Everything from education to entertainment to recreation would be a part of the city. Fuller also claimed that the low operating costs would result in a high standard of living. This is part of the document that Fuller wrote to convince the government about his ideas:
"In the early 1960s I was commissioned by a Japanese patron to design one of my tetrahedronal floating cities for Tokyo Bay. Three-quarters of our planet Earth is covered with water, most of which may float organic cities. Floating cities pay no rent to landlords. They are situated on the water, which they desalinate and recirculate in many usefuland non-polluting ways. They are ships with all an ocean ship's technical autonomy, but they are also ships that will always be anchored. They don't have to go anywhere. Their shape and its human-life accommodations are not compromised, as must be the shape of the living quarters of ships whose hull shapes are constructed so that they may slip, fishlike, at high speed through the water and high seas with maximum economy. Floating cities are designed with the most buoyantly stable conformation of deep-sea bell-buoys. Their omni-surface-terraced, slop-faced, tetrahedronal structuring is employed to avoid the lethal threat of precipitous falls by humans from vertically sheer high-rising buildings."
HUD eventually sent the plans to the U.S. Navy where they were dissected and analyzed even further. The city of Baltimore, upon hearing of the project, became interested and petitioned to have Triton City moored off of its shores in Chesapeake Bay. However, as municipal and federal administrations changed, the project languished and was never brought to light. Today, there are derivatives of Triton City — such as the artificial island Kansai and its airport in Osaka, Japan — but they pale in comparison to the scope of Triton City.
Preparation
Watch the video on test-driven development to learn to work with doctests. In doing so you will understand the two last statements in the skeleton of the source code that is given in this assignment.
Assignment
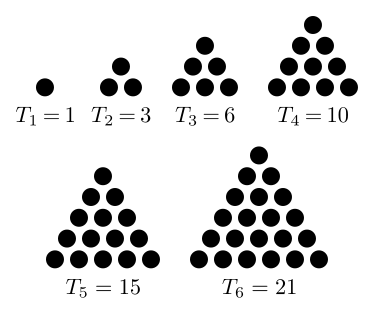
The factorial $n!$ of an integer $n \in \mathbb{N}$ is computed as the product of all strictly positive integers less than or equal to $n$. $$n! = \prod_{k=1}^{n}k = 1 \times 2 \times 3 \times \cdots \times n$$ According to the convention for an empty product, the value of $0! = 1$. The binomial coefficient $\binom{n}{k}$ This is an important statistic used in combinatorics that expresses the number of ways one can choose $k \in \mathbb{N}$ elements from a set of $n \in \mathbb{N}$ elements. $$\binom{n}{k} = \begin{cases}\frac{n!}{k!(n-k)!} & \mbox{als } 0 \leq k \leq n \\ 0 & \mbox{als } k \lt 0 \mbox{ of } k \gt n \end{cases}$$ The triangular number $T_n$ counts the number of circles that can form an equilateral triangle having $n \in \mathbb{N}$ circles on each side.
A triangular number is thus equal to the sum of all integers less than or equal to $n$. $$T_n = \sum_{k=1}^{n}k = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} = \binom{n+1}{2}$$ The tetrahedral number $P_n$ counts the number of spheres that can form a tetrahedron (a pyramid with a triangular base and three sides) having $n \in \mathbb{N}$ spheres on each side.
The $n$-th tetahedral number is thus equal to the sum of the first $n$ triangular numbers. $$P_n = \sum_{k=1}^{n}T_k = \frac{n(n+1)(n+2)}{6} = \binom{n+2}{3}$$ Below, we have already constructed the skeleton of the solution of this assignment. Your task is to implement the functions factorial, bionomialCoefficient, triangularNumber and tetrahedralNumber, so that they respectively compute the following properties: i) the factorial of $n$, the bionomial coefficient index by $n$ and $k$, iii) the $n$-th triangular number and iv) the $n$-th tetrahedral number. In all cases, $n$ and $k$ are positive integers.
def factorial(n): """ Computes the factorial of n. >>> factorial(10) 3628800 >>> factorial(32) 263130836933693530167218012160000000 """ def binomialCoefficient(n, k): """ Computes the bionomial coefficient index by n and k. >>> binomialCoefficient(7, 3) 35 >>> binomialCoefficient(12, 4) 495 """ def triangularNumber(n): """ Computes the n-th triangular number. >>> triangularNumber(10) 55 >>> triangularNumber(32) 528 """ def tetrahedralNumber(n): """ Computes the n-th tetrahedral number. >>> tetrahedralNumber(10) 220 >>> tetrahedralNumber(32) 5984 """ if __name__ == '__main__': import doctest doctest.testmod()
Example
>>> factorial(10) 3628800 >>> factorial(32) 263130836933693530167218012160000000 >>> binomialCoefficient(7, 3) 35 >>> binomialCoefficient(12, 4) 495 >>> triangularNumber(10) 55 >>> triangularNumber(32) 528 >>> tetrahedralNumber(10) 220 >>> tetrahedralNumber(32) 5984
Steden zijn al duizenden jaren een manifestatie van de kunstzinnigheid en verbeeldingskracht van de mensheid. Ze belichamen onze sterke sociale begeerte en hunkering naar het realiseren van grootse meesterwerken. Londen, Constantinopel, Parijs, New York, het oude Rome en Tokio zijn slechts enkele van de schitterende parels die de mensheid heeft opgebouwd. Maar er zijn ook evenveel voorbeelden te vinden van iemand's visie op een betere, efficiëntere en meer indrukwekkende stad die niet verder geraakt zijn dan een hoop gebroken dromen.
Buckminster Fuller was een briljante visionair, architect, wetenschapper, milieudeskundige en filosoof die in jaren 1960 met een gedurfd ontwerp voor een drijvende stad op de proppen kwam, die hij Triton City doopte (zie onderstaande foto). De stad zou opgebouwd worden uit tetraëdervormige modules, te beginnen met een drijvende buurt van 5000 inwoners met een basisschool, een supermarkt en een paar speciaalzaken. Uiteindelijk zouden drie tot vijf buurten een dorp vormen, en drie tot zeven dorpen een stad. Tijdens elke fase van de bouw zou er bijhorende infrastructuur worden toegevoegd: scholen, maatschappelijke voorzieningen, overheidsgebouwen en industrie. Een volledig opgebouwde stad zou plaats bieden aan 100.000 mensen in één enkel bouwwerk.
Fuller kreeg in eerste instantie een opdracht van een rijke Japanse beschermheer om een drijvende stad te ontwikkelen voor Tokyo Bay. De patron stierf echter in 1966, maar verassend genoeg kreeg Fuller een opdracht van het Amerikaanse ministerie van stedelijke ontwikkeling (HUD) voor de verdere ontwikkeling en analyse van zijn ontwerp. Fullers ontwerpen hielden onder andere rekening met het feit dat de steden bestand moesten zijn tegen tsunami's, zoveel mogelijk uitnodigden tot een buitenleven, zeewater konden ontzilten zodat het voor menselijke consumptie kon gebruikt worden, woningen zoveel mogelijk privacy moesten hebben, en gebruik gemaakt werd van tetraëdervormige modules omdat ze de grootst mogelijke oppervlakte aanbieden met het kleinst mogelijke volume. Alles, van opleiding tot amusement tot ontspanning zou deel uitmaken van de stad. Fuller beweerde ook dat de lage operationele kosten aanleiding zouden geven tot een hogere levensstandaard. Dit is een deel van het document waarmee Fuller de overheid kon overtuigen:
"In the early 1960s I was commissioned by a Japanese patron to design one of my tetrahedronal floating cities for Tokyo Bay. Three-quarters of our planet Earth is covered with water, most of which may float organic cities. Floating cities pay no rent to landlords. They are situated on the water, which they desalinate and recirculate in many usefuland non-polluting ways. They are ships with all an ocean ship's technical autonomy, but they are also ships that will always be anchored. They don't have to go anywhere. Their shape and its human-life accommodations are not compromised, as must be the shape of the living quarters of ships whose hull shapes are constructed so that they may slip, fishlike, at high speed through the water and high seas with maximum economy. Floating cities are designed with the most buoyantly stable conformation of deep-sea bell-buoys. Their omni-surface-terraced, slop-faced, tetrahedronal structuring is employed to avoid the lethal threat of precipitous falls by humans from vertically sheer high-rising buildings."
Uiteindelijk stuurde de HUD de plannen door naar de Amerikaanse marine, waar ze grondig werden ontleed en verder werden geanalayseerd. Toen de eerste geruchten over Triton City zich begonnen te verspreiden, raakte de stad Baltimore geïnteresseerd in het project en startte het een petitie om de stad te laten aanleggen aan de kust voor Chesapeake Bay. Veranderingen in het federale bestuur en dat van Baltimore zorgen er echter voor dat de plannen langzaam in de vergetelheid raakten en uiteindelijk nooit gerealiseerd werden. Vandaag de dag vinden we hier en daar flauwe afkooksels van Triton City — zoals het kunstmatige eiland Kansai (Japan) dat de luchthaven van Osaka huisvest — maar die verdwijnen in het niets bij de vooropgestelde omvang van het oorspronkelijke ontwerp.
Voorbereiding
Bekijk de video over test-driven development om te leren werken met doctests. Hierdoor zal je de laatste twee statements begrijpen in het skelet van de broncode dat wordt meegegeven met deze opgave.
Opgave
De faculteit $n!$ van een getal $n \in \mathbb{N}$ wordt berekend als het product van alle strikt positieve natuurlijke getallen die kleiner zijn dan of gelijk aan $n$. $$n! = \prod_{k=1}^{n}k = 1 \times 2 \times 3 \times \cdots \times n$$ Hierbij geldt dat $0! = 1$. De binomiaalcoëfficiënt $\binom{n}{k}$ is een grootheid uit de combinatoriek die aangeeft op hoeveel verschillende manieren men uit $n \in \mathbb{N}$ verschillende objecten er zonder terugleggen $k \in \mathbb{N}$ kan kiezen. $$\binom{n}{k} = \begin{cases}\frac{n!}{k!(n-k)!} & \mbox{als } 0 \leq k \leq n \\ 0 & \mbox{als } k \lt 0 \mbox{ of } k \gt n \end{cases}$$ Het driehoeksgetal $T_n$ stelt het aantal cirkels voor die een gelijkzijdige driehoek vormen met $n \in \mathbb{N}$ cirkels aan elke zijde.
Een driehoeksgetal is dus gelijk aan de som van alle natuurlijke getallen die kleiner zijn dan of gelijk aan $n$. $$T_n = \sum_{k=1}^{n}k = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} = \binom{n+1}{2}$$ Het tetraëdergetal $P_n$ stelt het aantal bollen voor die een tetraëder vormen (een piramide met een driehoekige basis en drie zijden) met $n \in \mathbb{N}$ bollen aan elke zijde.
Het $n$-de tetraëdergetal is gelijk aan de som van de eerste $n$ driehoeksgetallen. $$P_n = \sum_{k=1}^{n}T_k = \frac{n(n+1)(n+2)}{6} = \binom{n+2}{3}$$ We hebben hieronder reeds het skelet opgemaakt voor de oplossing van deze opgave. Je taak bestaat erin de functies faculteit, binomiaal, driehoeksgetal en tetraedergetal te implementeren, zodat ze respectievelijk de volgende eigenschappen berekenen: i) de faculteit van $n$, ii) de bionomiaalcoëfficiënt van $n$ over $k$, iii) het $n$-de driehoeksgetal en iv) het $n$-de tetraëdergetal. Hierbij zijn $n$ en $k$ natuurlijke getallen.
def faculteit(n): """ Berekent de faculteit van het natuurlijk getal n. >>> faculteit(10) 3628800 >>> faculteit(32) 263130836933693530167218012160000000 """ def binomiaal(n, k): """ Berekent de binomiaalcoëfficiënt van n over k. >>> binomiaal(7, 3) 35 >>> binomiaal(12, 4) 495 """ def driehoeksgetal(n): """ Berekent het n-de driehoeksgetal. >>> driehoeksgetal(10) 55 >>> driehoeksgetal(32) 528 """ def tetraedergetal(n): """ Berekent het n-de tetraëdergetal. >>> tetraedergetal(10) 220 >>> tetraedergetal(32) 5984 """ if __name__ == '__main__': import doctest doctest.testmod()
Voorbeeld
>>> faculteit(10) 3628800 >>> faculteit(32) 263130836933693530167218012160000000 >>> binomiaal(7, 3) 35 >>> binomiaal(12, 4) 495 >>> driehoeksgetal(10) 55 >>> driehoeksgetal(32) 528 >>> tetraedergetal(10) 220 >>> tetraedergetal(32) 5984
| Added by: | Peter Dawyndt |
| Date: | 2015-10-08 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |



 RSS
RSS