PWSUM - Power Sums
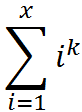
Everyone knows that we can express sums this form as polynomials of degree k+1. Most people find it hard to derive actual formulas for such sums, so we'd like to have a program that does that for us! You are given a non-negative integer K, and you're asked to compute the coefficient representation of the polynomial which defines the sum shown above. However, we'd like to simplify your computation so you only have to output the formula modulo 10007. (A formula which correctly computes the remainder of the sum when divided by 10007, for any natural x).
Input
The first and only line of input contains a nonnegative integer k (0 <= k <= 300): the power we use in our sum.
Output
The first and only line of output should contain the canonic coefficient representation of the formula. To elaborate, this should be the form of your output:
ak+1xk+1 + akxk + ak-1xk-1 ... a0x0
ai here represents the coefficient that stands by the i-th power of x. As we only wish to find the formula modulo 10007, all the coefficients should be from interval [0, 10006] of integers. See the sample input and output for further clarification.
Example
Input: 1 Output: 5004x^2 + 5004x^1 + 0x^0
Input: 3 Output: 2502x^4 + 5004x^3 + 2502x^2 + 0x^1 + 0x^0
hide comments
|
|
sankalp_7:
2024-02-23 15:27:16
Is there any concept required to solve this problem? |
|
|
Chad Sang:
2014-11-15 12:01:35
@Mitch Schwartz: Thanks! Do you mean when k = 4, the output should be "3002x^5 + 6005x^4 + 6333x^3 + 550x^2 + 7276x^1 + 0x^0" ?
|
|
|
Mitch Schwartz:
2014-11-15 03:59:16
@Chad Sang: The polynomial is meant to be evaluated modulo 10007. In other words, you can plug your value of x into the formula and then find the remainder of the result when divided by 10007, and it will match the remainder you would get if you computed the sum directly, for any natural x. Last edit: 2014-11-15 04:04:37 |
|
|
Chad Sang:
2014-11-15 03:50:14
What's the meaning of
|
|
|
Gaurav Kumar Verma:
2014-10-16 23:28:20
can any please help me understand the question??? |
| Added by: | gustav |
| Date: | 2010-06-30 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: PERL6 |
| Resource: | own problem |

 RSS
RSS