PZPI5 - Nadruk na płytce
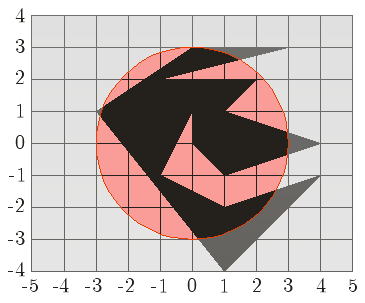
A well known music producer in Byteland is currently designing the cover of its latest album of a black metal band. The task was commissioned to the avant-garde hacker artist j0hnny, and he has just handed in his work of art to the producer. This work of art, on closer inspection, turns out to be a polygon scribbled on a sheet of paper and completely filled in with black ink.
Surprisingly, the cover has received a favorable reception from the fans, and the producer intends to print the same work of art on the top side of the CD itself. However, the polygon is a little irregular, so it will have to be truncated to fit the circular shape of the disc.
Since the specific black ink to be used on the CD is extremely expensive, a cost estimate needs to be made before the printing. Please calculate exactly how much ink will be used on each CD.
Input
The first line of input contains an integer t (t<=20). The descriptions of t testcases follow.
Each testcase starts with a line containing two integers: n r, denoting the number of the vertices on the outer boundary of j0hnny's polygon and the radius of the circle representing the CD, respectively (3<=n<=100000, 1<=r<=20000). The CD is assumed to be centered at the origin (0,0) of the coordinate system. The next n lines contain two integers xi yi representing the X and Y coordinates of the successive vertices of j0hnny's polygon, ordered clockwise (-20000 <= xi,yi<= 20000).
Output
For each testcase print exactly one number, equal to the area of the part of the polygon which is contained within the disc. The computed result must be accurate up to a maximum error of 0.01.
Example
Input: 1 14 3 1 -1 0 0 0 1 -1 -1 1 -2 4 -1 1 -4 -3 1 0 3 3 3 -1 2 2 2 1 1 4 0 Output: 15.6515
| Added by: | adrian |
| Date: | 2005-05-21 |
| Time limit: | 1.904s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | I Pomorskie Zawody w Programowaniu Indywidualnym - finał |

 RSS
RSS